1) чем больше ставка дисконтирования, тем меньше приведенная стоимость, и наоборот;
2) чем меньше срок инвестиции, тем больше приведенная стоимость, и наоборот.
Приведенная стоимость потока денежных платежей определяется в виде суммы приведенных стоимостей платежей, образующих этот денежный поток.
Пример 1.6. Финансовый директор компании знает, что ему предстоит произвести следующие платежи:

Какую денежную сумму необходимо инвестировать сегодня, чтобы обеспечить выполнение обязательств, если процентная ставка равна 6 % при начислении процентов дважды в год?
Достаточно определить приведенную стоимость данного потока платежей:
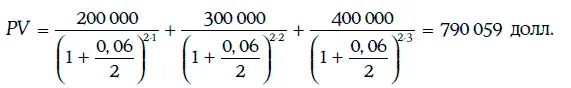
Если денежный поток представляет собой обыкновенную ренту, по которой т раз в год в течение Т лет выплачивается одна и та же денежная сумма А, то приведенная стоимость такой ренты может быть найдена следующим образом:
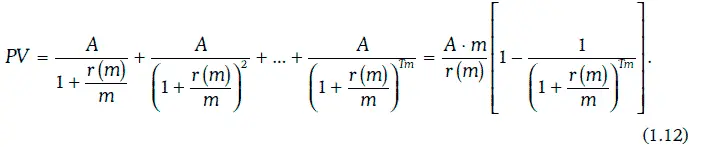
Пример 1.7.Банк согласился предоставить 30-летний ипотечный кредит в размере 100 000 долл. По условиям ипотечного кредитования ежемесячные платежи заемщика должны быть одинаковыми. Годовая процентная ставка, требуемая банком, равна 12 %. Какова величина ежемесячного платежа заемщика?
Величина ежемесячного платежа заемщика определяется из условия, что приведенная стоимость потока платежей заемщика должна составить 100 000 долл. Значит,
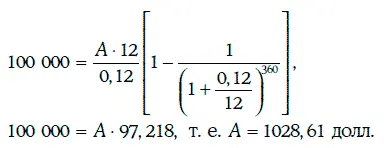
Обыкновенную ренту называют бессрочной [14] Другое название – перпетуитет ( perpetuity ).
(perpetual annuity), если поток рентных платежей не ограничен по времени. Приведенная стоимость бессрочной ренты, по которой m раз в год выплачивается сумма А, может быть найдена следующим образом:
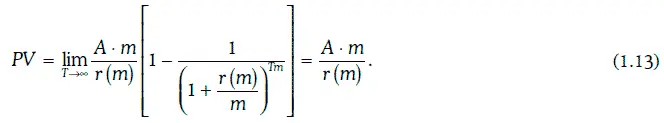
1.4. Внутренняя доходность финансовых инструментов
Внутренней доходностью (internal rate of return – IRR) финансового инструмента называют процентную ставку, при которой приведенная стоимость потока платежей по данному финансовому инструменту совпадает с его рыночной ценой.
Пример 1.8.Финансовый инструмент продается по цене 1243,82 долл., и по нему каждые 6 месяцев выплачивается по 50 долл. в течение 5 лет и еще 1000 долл. в конце пятого года. Покажем, что внутренняя доходность данного финансового инструмента при начислении процентов дважды в год составляет 4,5 %.
Приведенная стоимость денежного потока по данному финансовому инструменту определяется следующим образом:
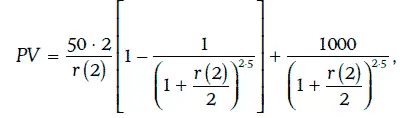
где r(2) – годовая процентная ставка при начислении процентов дважды в год.
При r(2) = 0,045 имеем
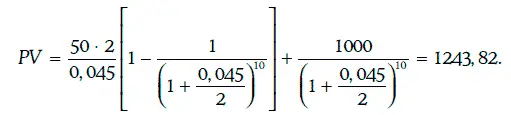
Так как приведенная стоимость денежного потока, определяемого финансовым инструментом, совпала с его рыночной ценой, то внутренняя доходность этого инструмента действительно равна 4,5 %.
Рассмотрим финансовый инструмент со следующим потоком платежей:

Внутренняя доходность рассматриваемого финансового инструмента при начислении процентов m раз в год является решением уравнения:
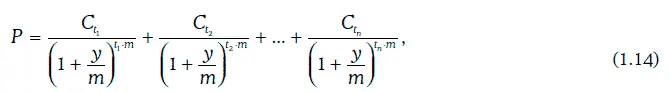
где Р – рыночная цена финансового инструмента.
Функция 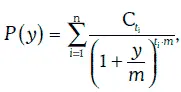 стоящая в правой части уравнения (1.14), всегда является убывающей и выпуклой. График функции изображен на рис. 1.1.
стоящая в правой части уравнения (1.14), всегда является убывающей и выпуклой. График функции изображен на рис. 1.1.
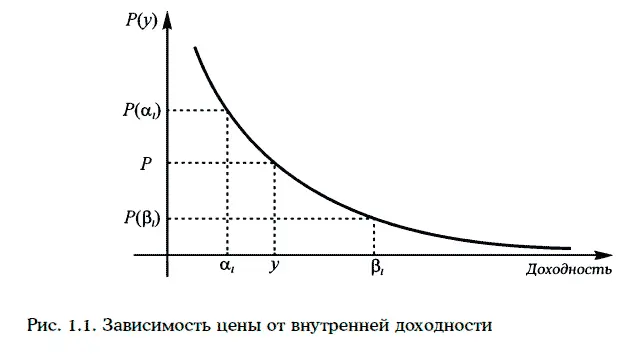
Для решения уравнения (1.14) можно использовать метод проб и ошибок. Вначале найдем простым подбором числа α 1и β 1так, чтобы P(α 1) > Р, а P(β 1) < Р (рис. 1.2). Тогда искомая внутренняя доходность будет находиться между α 1и β 1, т. е. у ∈ (α 1, β 1). Промежуток (α 1, β 1) разделим на 10 равных частей. И, вычисляя значение функции Р(у) в точках деления, найдем числа α 2и β 2так, чтобы:
Читать дальше


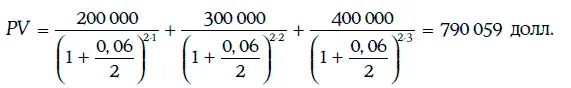
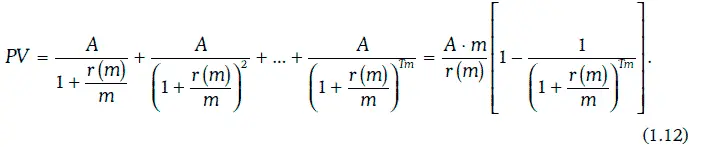
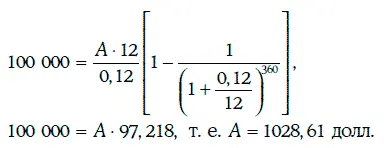
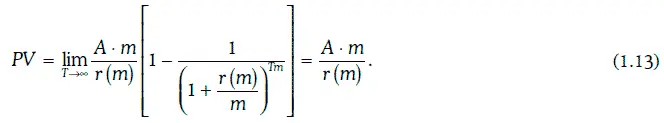
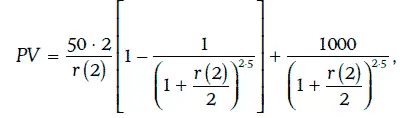
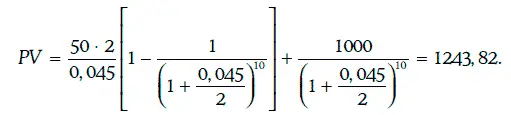

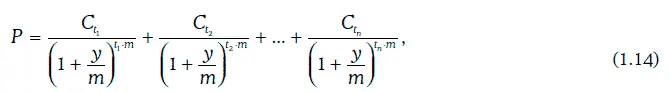
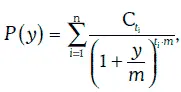 стоящая в правой части уравнения (1.14), всегда является убывающей и выпуклой. График функции изображен на рис. 1.1.
стоящая в правой части уравнения (1.14), всегда является убывающей и выпуклой. График функции изображен на рис. 1.1.











