Петр Путенихин - Правила счета элементов бесконечного множества

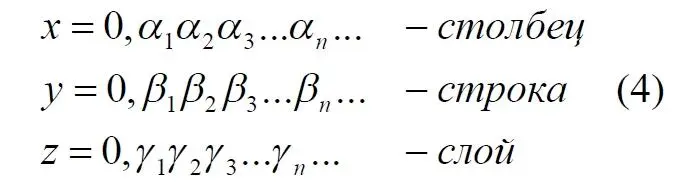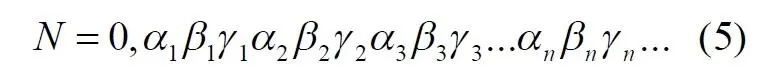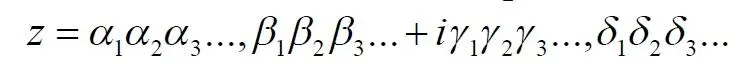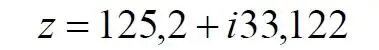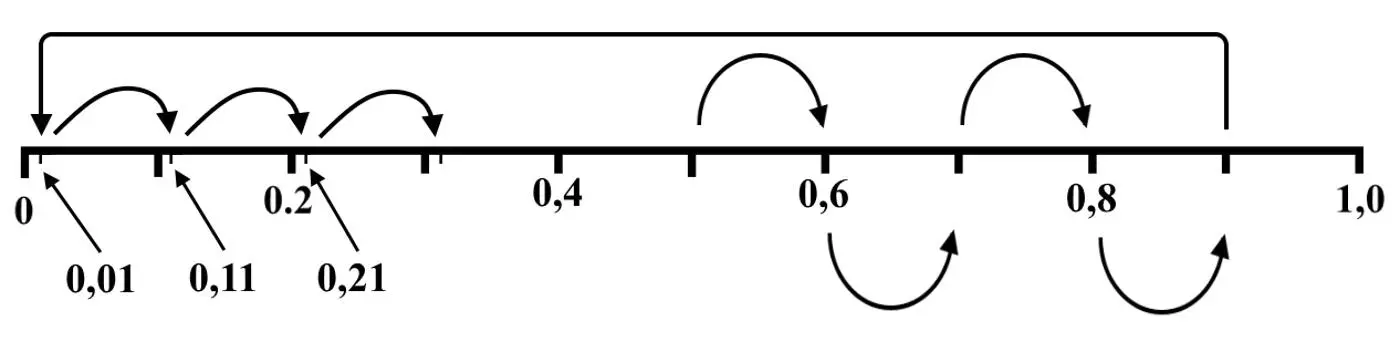
Рис.2. Нумерация точек отрезка

На рисунке показан фрагмент последовательной нумерации точек, начиная с точки 0,5 и заканчивая на точке 0,31. Мы последовательно рассматриваем фрагмент, точки с натуральными порядковыми номерами 5, 6, 7, 8, 9, 10, 11, 12, 13, по которым из выражения (3) определяем значения этих точек: 0,5 (точка номер 5); 0,6 (точка номер 6); 0,7 (точка номер 7 и так далее); 0,8; 0,9; 0,01 (точка номер 10); 0,11; 0,21; 0,31 (точка номер 13). Как видим, порядковые номера точек равномерно возрастают, но сами точки при этом "скачут" по линии. Отметим главное: фактическое значение точки "возникает" в самом процессе нумерации. То есть, сначала мы выбираем некоторый или очередной, натуральный порядковый номер точки, а затем определяем её местоположение на линии и присваиваем этой точке выбранный номер.

Собственно говоря, нумерация элементов массива и означает присвоение конкретному элементу некоторого определенного номера, как бы навешивание на элемент таблички с номером. Поэтому выбрав элемент, мы можем увидеть его номер, а выбрав номер, узнать, какому элементу он принадлежит. В рассмотренном случае с нумерацией точек линии натуральный порядковый номер, например, 12 389 принадлежит точке на линии со значением 0,98321. Наоборот, точка линии со значением, например, 0,5612999 имеет в массиве порядковый номер 9 992 165.

Такой же алгоритм можно использовать и для нумерации точек плоских или объемных, многомерных объектов, например, точек куба. В случае многомерных объектов номер преобразуется к виду (3) по методу Кантора, созданного им для отождествления точек линии и квадрата [3, с.77].

Предположим, некая точка куба имеет следующие координаты, в которых буквы α, β и γ обозначают любую цифру в этих числах:

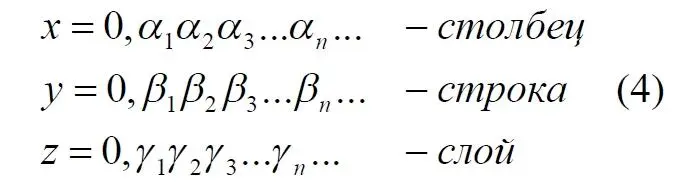
Используя метод Кантора, формируем из этих чисел новое число:

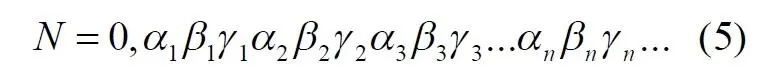
Отсутствующие цифры для какого-либо индекса заменяем нулями. Дробную часть полученного комбинированного числа инвертируем, поворачиваем "задом наперед", согласно (3), и получаем натуральный порядковый номер рассмотренной точки куба. Например, точка куба с координатами p(x, y, z) = (0,123; 0,321; 0,9171) при комбинировании даст число N=139 221 317 001, что означает порядковый номер точки в бесконечном их массиве, равный 100 713 122 931. Понятно, что обратным преобразованием можно так же найти координаты любой точки по её номеру. Например, точка с порядковым номером 1 234 567 890 имеет в кубе координаты p(0,0741; 0,963; 0,852). Рассмотренный вариант относится к кубу с единичным ребром, но он может быть легко расширен на куб с любым размером ребра, а также на объекты вообще с любым числом измерений.

Наконец, метод позволяет перенумеровать и составные элементы: комплексные числа, кватернионы и тому подобные. Например, комплексное число можно представить в виде

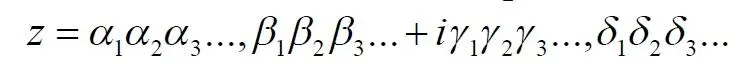
В этой записи буквами α и γ обозначены целая часть числа реальной и мнимой части, а буквами β и δ, соответственно, их дробные части. Например:

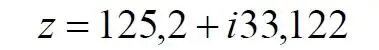
Количество цифр α, β, γ и δ в записях может быть любым. Теперь, используя метод комбинации, можно получить число N, инверсная запись которого и будет обозначать натуральный порядковый номер этого числа в их бесконечном массиве. Например, приведенное выше комплексное число будет иметь в бесконечном массиве всех возможных комплексных чисел натуральный порядковый номер 200 123 021 325. Кстати, можно заметить, что в таком массиве первые 10 чисел (0…9) являются реальными, а число i (комплексная единица) находится на позиции 100 и имеет порядковый номер 10. Также заметим, что при таком подходе основой всех чисел являются вещественные числа, а различные комплексные и им подобные – это простая комбинация этих базовых чисел. Условно говоря – все эти комбинационные числа являются своеобразной тенью, миражом чисел реальных.

Нетрудно заметить, что нумерация комплексных чисел тождественна нумерации точек квадрата. В этих частных случаях можно легко применить для их нумерации традиционный диагональный процесс Кантора.