Петр Путенихин - Правила счета элементов бесконечного множества

Перенумеровать или, тождественно, пересчитать бесконечное количество чего-либо, в том числе, сосчитать точки отрезка, действительно, невозможно физически. Однако приводимое затем доказательство, как правило, начинается со слов: «Представим, что вопреки нашему утверждению кому-то удалось перенумеровать точки этого отрезка», после чего приводятся хитрые комбинации с нумерацией. Но здесь следует напомнить фундаментальный принцип классической логики и классической математики, который постулирует полное отрицание актуальной бесконечности: «Infinitum Actu Non Datur » (Аристотель) – «актуальная бесконечность не существует». Принцип утверждает потенциальный, т.е. принципиально незавершаемый характер бесконечности множества. Актуальная, то есть, пересчитанная бесконечность лишена смысла. Бесконечностью может считаться лишь потенциальная бесконечность, завершить счет членов которой невозможно. Поэтому приводимое доказательство на этих словах можно и прервать – оно некорректно с самого начала. Впрочем, в этом вопросе особое мнение, которое следует признать некорректным, приписывается Давиду Гильберту. По мнению немецкого математика, одного из величайших умов своего времени, главное различие между актуальной и потенциальной бесконечностью заключается в следующем. Потенциально бесконечное есть всегда нечто возрастающее и имеющее пределом бесконечность, тогда как актуальная бесконечность – это завершённое целое, в действительности содержащее бесконечное число предметов [5].

В литературе можно встретить описание довольно интересного способа подсчета количества точек на отрезке линии. Нетрудно догадаться, что в этом примере использованная методика счета ошибочна и ведет к ошибочному выводу. Несложное доказательство несчетности содержит не очень сильно скрытую подмену понятий. Итак:

"Теперь уже несложно доказать, что множество всех точек на прямой линии несчетно. Вместо этого множества можно говорить о множестве всех действительных чисел, так как каждой точке прямой соответствует действительное число и обратно. Каждое действительное число можно записать в виде бесконечной десятичной дроби вида α,α 1α 2α 3…α n…" [3, с.73-74].

Как видим, ряд знаков имеет бесконечное счетное количество знаков и, резонно предположим, что так же считает и автор доказательства. Сразу же заметим, что утверждения следует признать абсурдными. Любое конечное число всегда меньше бесконечности.

"Предположим, что нам удалось каким-то образом перенумеровать все действительные числа. Чтобы доказать, что это предположение неверно, достаточно построить хоть одно незанумерованное число. … поступим следующим образом. Сначала напишем нуль и поставим после него запятую. Потом возьмем число, получившее первый номер, и посмотрим на его первый десятичный знак после запятой (то есть на число десятых)" [там же].

Для определенности отметим, что поиск незанумерованного числа производится, как можно заметить, на отдельном интервале всех действительных чисел [0, 1]. Сначала как на неточность в этом рассуждении, как и в предыдущем доказательстве, сразу же укажем на очевидное, но, похоже, незамеченное обстоятельство: на самом деле при последовательном, возрастающем счёте у второго числа вторая цифра тоже будет 0. И у третьего. И у четвертого. И у числа, занимающего бесконечно большую позицию. На словах это, возможно, не совсем ясно, поэтому покажем это на "виновнике торжества" – на оцифрованном отрезке:

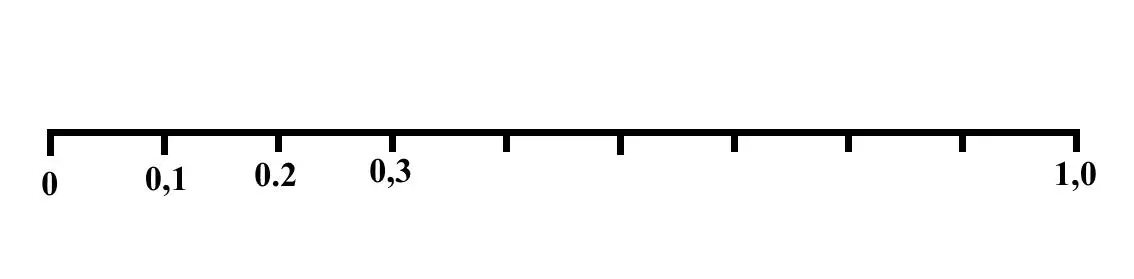
Рис.1. Оцифрованный отрезок, отдельный интервал всех действительных чисел

На рисунке видно, что первая цифра после нуля будет отличной от нуля, единица будет только после точки 0,1 отрезка. На интервале от 0 до 0,1 содержится счетное (пока оспариваемое) количество точек. Во всяком случае, это не одна, не миллион и даже не гугл точек, равный 10 100, а в бесконечное число раз больше. У всех этих чисел первой цифрой после запятой будет ноль. Следовательно, искомое число пока находится вблизи нулевой точки, в самом начале отрезка [0, 1].

"Если эта цифра отлична от 1, то в числе, которое мы пишем, поставим после запятой 1, а если эта цифра равна 1, то поставим после запятой 2" [3, с.73-74].

Еще раз отметим, что отличная от единицы цифра в первой позиции после нуля первого числа будет нулем. Следовательно, в "искомом" числе после запятой первой будет 2. То есть, число будет 0,2. Сразу же на рисунке находим, что эта точка на отрезке есть – это точка 0,2.