Петр Путенихин - Правила счета элементов бесконечного множества

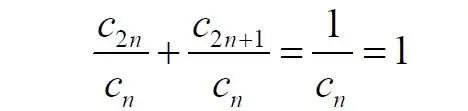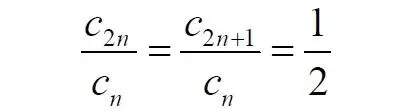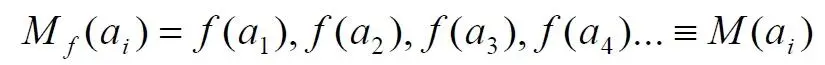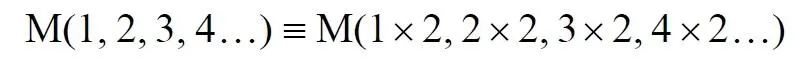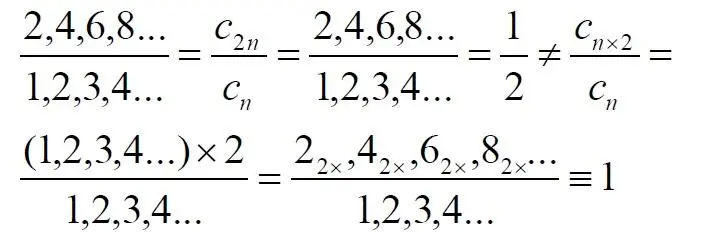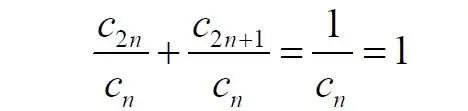
Поэтому из равенства также следует, что каждая из мощностей четных и нечётных чисел в два раза «слабее» мощности всех натуральных чисел:

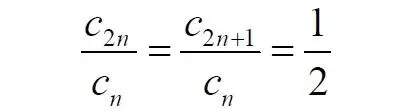
Отметим также без доказательств, что любые действия над каждым членом множества не изменяют мощности множества:

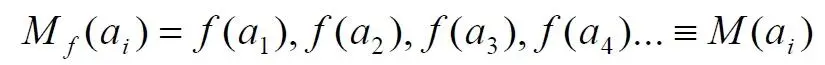
Из этого непосредственно следует, что решающее значение имеет способ, каким получено множество. Например, множество всех четных чисел может быть получено удалением из множества всех натуральных чисел нечётных или умножением на 2 каждого члена множества всех натуральных чисел:

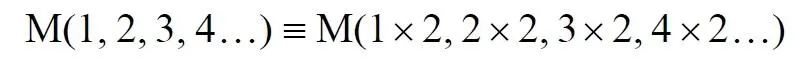
Казалось бы, последнее выражение является точной копией множества всех четных чисел М(2, 4, 6, 8…). Но это ошибочно, поскольку любые действия над всеми (или отдельными) членами множества не изменяют их полного количества и, соответственно, мощности. Поэтому справедливо (знак множества M опускаем):

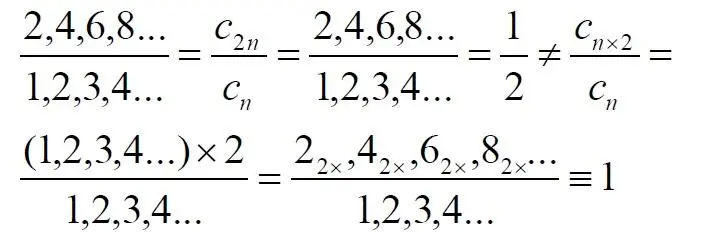
Хотя оба множества в числителях в обеих строках выглядят тождественно, на самом деле это разные множества, имеющие разную мощность.

Перестановки в рядах . Еще один вариант доказательства равномощности части и целого приведен в книге [2, с.282], где предлагается вести подсчет нечетных чисел, предварительно переставив их в ряду:

"В бесконечной вселенной коэффициент объема можно определить как долю, занятую областями данного типа. Но это определение приводит к неоднозначности. Чтобы проиллюстрировать природу проблемы, зададимся вопросом: какова доля нечетных чисел среди целых? Четные и нечетные числа чередуются в последовательности 1, 2, 3, 4, 5, и можно подумать, что ответом, очевидно, будет половина. Однако целые числа можно упорядочить другим способом. Например, так: 1, 2, 4, 3, 6, 8 … Эта последовательность по-прежнему включает все целые числа, но теперь за каждым нечетным числом следует два четных, и кажется, что только треть целых чисел являются нечетными"

Здесь нам отчетливо видна некорректность и противоречивость такой модификации числового ряда, которая строго последовательно и логично легко доводится до абсурда. Для этого все нечетные числа поместим в самый конец бесконечной последовательности. Теперь при поверхностном анализе последовательности мы обнаружим, что в ней нечетных чисел нет вообще. Конечно, мы догадываемся, что все они где-то дальше, но, как бы долго мы ни просматривали последовательность, мы никогда не встретим в ней ни одного нечетного числа. Однако итог явно абсурден: нечетные числа точно есть, но мы их почему-то не пересчитываем. Причина заключается просто в выборе метода подсчета: игнорирование длины ряда. Мы же сами каким-то образом перенесли нечетные числа в конец ряда? Ну, так и нумеровать тогда следует весь ряд. Это же относится и к предложенному выше методу упорядочивания. Каким-то образом эти числа перетасованы? Вплоть до последнего. Ну, так и считать следует соответственно – до последнего числа. Если же числа перетасовываются в процессе счета, тогда "временно вынутые из ряда нечетные числа" все время будут где-то скапливаться. Трудно будет не заметить это бесконечно большое хранилище нечетных чисел.

С другой стороны, мы можем проделать то же самое и с четными числами, например, получив в результате, что их в общем ряду только треть. Иначе говоря, один и тот же метод показывает, что среди целых чисел нечетных одновременно только половина и только две трети. Понятно, что методика, дающая два взаимоисключающих результата не вызывает доверия.

Группировка степеней . Такие методики пересчета, отождествления всегда содержат плохо скрытую подмену понятий. Например, с рядом натуральных чисел отождествляется ряд степеней 10 1, 10 2, 10 3… 10 n… и так далее. Таким же образом устанавливается взаимно однозначное соответствие и между множеством натуральных чисел и множеством всех квадратов натуральных чисел 1 2, 2 2, 3 2, … n 2… и так далее. Но принять такое отождествление нет никаких оснований.