
Но большинство людей делит пиццы совсем не так. Третья часть пиццы слишком велика и часто складывается, когда вы берете ее в руки. Вместо этого мы, повинуясь инстинкту, делим пиццу на шесть частей и раздаем каждому по две. То, что две шестых доли и одна третья – одно и то же, настолько очевидно, что нет, кажется, никакой необходимости даже проговаривать это. Тем не менее этот факт – основа принципа упрощения дробей и сведения их к простейшему виду: 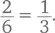 Упрощение дробейвстречается в математике повсеместно, и владение этим навыком делает очень многие вычисления гораздо проще.
Упрощение дробейвстречается в математике повсеместно, и владение этим навыком делает очень многие вычисления гораздо проще.
Ключ к упрощению дробей – найти числа, на которые делились бы одновременно и числитель, и знаменатель дроби ( наибольший общий делитель). Положим, надо упростить 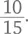
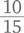 И числитель, и знаменатель этой дроби делятся на пять. Поэтому
И числитель, и знаменатель этой дроби делятся на пять. Поэтому 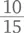 – то же, что
– то же, что 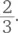
Или можно записать числитель и знаменатель в виде произведения, так что:
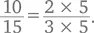
При такой записи дроби найти простейший ее вид намного проще; нужно вычеркнуть числа, которые встречаются и в числителе, и в знаменателе (в данном случае вычеркиваем пятерки и получаем 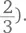
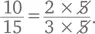
(Если вам не нравится мысль о том, что что-то там зачеркивается, существует и другой способ. 2 × 5: 3 × 5 это то же самое, что 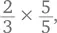 что равно
что равно 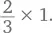 При такой записи очевидно, что ничто волшебным образом не пропадает, но расчет сильно упрощается.)
При такой записи очевидно, что ничто волшебным образом не пропадает, но расчет сильно упрощается.)
Игра: усложненные дроби
Прежде чем начинать по-настоящему работать с ребенком над упрощением дробей, может быть полезно начать с их усложнения! На помощь снова приходит игра – придумывание все более сложных методов разрезания пиццы: любая 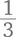 может оказаться
может оказаться 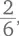 или
или 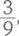 или
или 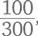 или даже
или даже 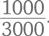 Насколько тонкими будут ломтики пиццы? Смысл этого глупого занятия – дать ребенку возможность привыкнуть к идее о том, что разные дроби могут в реальности представлять одну и ту же величину. Это сложная идея. К примеру, наша позиционная система записи чисел означает, что цифры в числах 36 и 12 означают очень разные величины, но те же цифры в дробях
Насколько тонкими будут ломтики пиццы? Смысл этого глупого занятия – дать ребенку возможность привыкнуть к идее о том, что разные дроби могут в реальности представлять одну и ту же величину. Это сложная идея. К примеру, наша позиционная система записи чисел означает, что цифры в числах 36 и 12 означают очень разные величины, но те же цифры в дробях 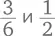 означают в точности одно и то же количество. Так что игра, в ходе которой ребенок привыкает к тому, что дроби можно сделать более сложными, но при этом их величина не меняется, помогает подготовить почву для размышлений о том, нельзя ли сложным дробям придать более простой вид.
означают в точности одно и то же количество. Так что игра, в ходе которой ребенок привыкает к тому, что дроби можно сделать более сложными, но при этом их величина не меняется, помогает подготовить почву для размышлений о том, нельзя ли сложным дробям придать более простой вид.
Проверьте себя
26. Громадная дробь для упрощения
Упростите эту дробь путем вычеркивания чисел над и под чертой:
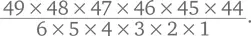
Некоторые дроби очень трудно сравнивать. Так, при помощи метода деления сосисок невозможно оказалось определить, что больше – 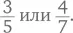 В данном случае единственный способ разобраться сводится к использованию метода шоколадки. Представьте, что у вас есть шоколадка, которую вы можете разделить на пять и семь равных частей. Это означает, что число кусочков в шоколадке должно делиться на 5 и на 7. Следовательно, плитка шоколада должна иметь пять «строк» и семь «столбцов», примерно так:
В данном случае единственный способ разобраться сводится к использованию метода шоколадки. Представьте, что у вас есть шоколадка, которую вы можете разделить на пять и семь равных частей. Это означает, что число кусочков в шоколадке должно делиться на 5 и на 7. Следовательно, плитка шоколада должна иметь пять «строк» и семь «столбцов», примерно так:
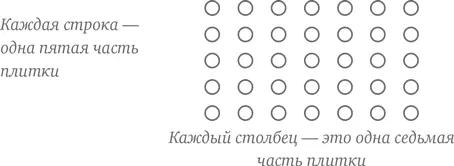
При этом в плитке всего 5 × 7, или 35 кусочков. Теперь несложно разобраться, сколько кусочков составляет 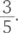 Это три пятых, то есть три строки – 21 кусочек.
Это три пятых, то есть три строки – 21 кусочек. 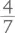 – это четыре седьмых, четыре столбца, 20 кусочков. Таким образом,
– это четыре седьмых, четыре столбца, 20 кусочков. Таким образом, 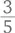 больше (чуть-чуть!), чем
больше (чуть-чуть!), чем 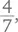 потому что
потому что 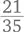 больше, чем
больше, чем 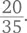
Читать дальше
Конец ознакомительного отрывка
Купить книгу


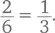 Упрощение дробейвстречается в математике повсеместно, и владение этим навыком делает очень многие вычисления гораздо проще.
Упрощение дробейвстречается в математике повсеместно, и владение этим навыком делает очень многие вычисления гораздо проще.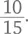
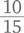 И числитель, и знаменатель этой дроби делятся на пять. Поэтому
И числитель, и знаменатель этой дроби делятся на пять. Поэтому 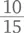 – то же, что
– то же, что 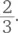
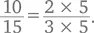
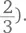
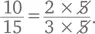
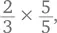 что равно
что равно 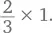 При такой записи очевидно, что ничто волшебным образом не пропадает, но расчет сильно упрощается.)
При такой записи очевидно, что ничто волшебным образом не пропадает, но расчет сильно упрощается.)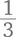 может оказаться
может оказаться 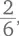 или
или 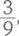 или
или 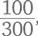 или даже
или даже 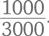 Насколько тонкими будут ломтики пиццы? Смысл этого глупого занятия – дать ребенку возможность привыкнуть к идее о том, что разные дроби могут в реальности представлять одну и ту же величину. Это сложная идея. К примеру, наша позиционная система записи чисел означает, что цифры в числах 36 и 12 означают очень разные величины, но те же цифры в дробях
Насколько тонкими будут ломтики пиццы? Смысл этого глупого занятия – дать ребенку возможность привыкнуть к идее о том, что разные дроби могут в реальности представлять одну и ту же величину. Это сложная идея. К примеру, наша позиционная система записи чисел означает, что цифры в числах 36 и 12 означают очень разные величины, но те же цифры в дробях 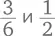 означают в точности одно и то же количество. Так что игра, в ходе которой ребенок привыкает к тому, что дроби можно сделать более сложными, но при этом их величина не меняется, помогает подготовить почву для размышлений о том, нельзя ли сложным дробям придать более простой вид.
означают в точности одно и то же количество. Так что игра, в ходе которой ребенок привыкает к тому, что дроби можно сделать более сложными, но при этом их величина не меняется, помогает подготовить почву для размышлений о том, нельзя ли сложным дробям придать более простой вид.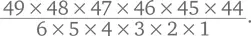
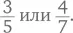 В данном случае единственный способ разобраться сводится к использованию метода шоколадки. Представьте, что у вас есть шоколадка, которую вы можете разделить на пять и семь равных частей. Это означает, что число кусочков в шоколадке должно делиться на 5 и на 7. Следовательно, плитка шоколада должна иметь пять «строк» и семь «столбцов», примерно так:
В данном случае единственный способ разобраться сводится к использованию метода шоколадки. Представьте, что у вас есть шоколадка, которую вы можете разделить на пять и семь равных частей. Это означает, что число кусочков в шоколадке должно делиться на 5 и на 7. Следовательно, плитка шоколада должна иметь пять «строк» и семь «столбцов», примерно так:
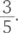 Это три пятых, то есть три строки – 21 кусочек.
Это три пятых, то есть три строки – 21 кусочек. 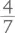 – это четыре седьмых, четыре столбца, 20 кусочков. Таким образом,
– это четыре седьмых, четыре столбца, 20 кусочков. Таким образом, 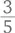 больше (чуть-чуть!), чем
больше (чуть-чуть!), чем 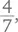 потому что
потому что 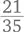 больше, чем
больше, чем 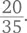







![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



