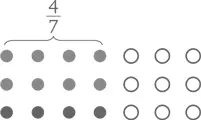
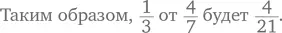
Алгоритм решения любых подобных примеров (таких как 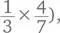 выглядит так:
выглядит так:
• перемножить числители (в данном случае 1 × 4 = 4);
• перемножить знаменатели (в данном случае 3 × 7 = 21).
Записывается это так:
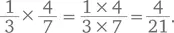
Чему равно 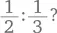
Не правда ли, сразу всплывают какие-то неопределенные (или вполне отчетливые) воспоминания о том, что что-то нужно «перевернуть»? Одна американская мама рассказала нам, что у них для запоминания этого правила был даже какой-то стишок. Может быть, такой: «Делить на дробь – пустяшное дело: переверни – и умножай смело».
Таким образом:

Все так, если вы уверены, что правило верное и ему надо следовать. Но подумайте вот о чем. Мы начинали с 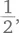 а закончили
а закончили 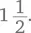 Реакция большинства людей на этот пример была бы приблизительно такой: «Ну вот, посмотрите, что получается. С этого момента математика перестает опираться на здравый смысл».
Реакция большинства людей на этот пример была бы приблизительно такой: «Ну вот, посмотрите, что получается. С этого момента математика перестает опираться на здравый смысл».
Давайте перенесем этот абстрактный пример в реальную жизненную ситуацию. Предположим, в рецепте приготовления теста для блинов предлагается на определенное количество блинчиков взять 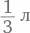 молока (не думайте о других ингредиентах – яйцах, муке и пр.). Сколько таких порций теста вы сможете изготовить из целого литра молока? Три.
молока (не думайте о других ингредиентах – яйцах, муке и пр.). Сколько таких порций теста вы сможете изготовить из целого литра молока? Три.
Откуда вам это известно? Это потому, что 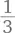 литра входит в литр трижды. Точно так же, как именно благодаря делению
литра входит в литр трижды. Точно так же, как именно благодаря делению 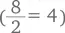 вы знаете, что «2 укладывается в 8 четыре раза», тот факт, что
вы знаете, что «2 укладывается в 8 четыре раза», тот факт, что 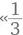 литра входит в литр трижды», тоже становится очевиден в результате деления:
литра входит в литр трижды», тоже становится очевиден в результате деления: 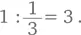
Теперь ответ в примере 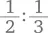 становится понятнее:
становится понятнее:

Десятичные дроби и проценты
Десятичные дроби и проценты часто рассматриваются как что-то отличное от обычных дробей, таких как 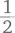 или
или 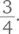 Отчасти это объясняется тем, что они иначе выглядят: действительно, 0,5 или 50 % совсем не похоже на
Отчасти это объясняется тем, что они иначе выглядят: действительно, 0,5 или 50 % совсем не похоже на 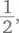 но смысл во всех трех записях содержится совершенно одинаковый. Зачем же тогда запутывать ситуацию и придумывать разные способы обозначения? Если все это просто
но смысл во всех трех записях содержится совершенно одинаковый. Зачем же тогда запутывать ситуацию и придумывать разные способы обозначения? Если все это просто 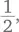 то почему всегда так и не писать? Причина в том, что десятичные дроби намного проще сравнивать и удобнее проводить с ними расчеты. Помните, как трудно было сравнивать
то почему всегда так и не писать? Причина в том, что десятичные дроби намного проще сравнивать и удобнее проводить с ними расчеты. Помните, как трудно было сравнивать 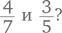 Так вот, если прибегнуть к помощи десятичных дробей и процентов, процедура сравнения стала бы намного проще.
Так вот, если прибегнуть к помощи десятичных дробей и процентов, процедура сравнения стала бы намного проще.
В голове ребенка
Расположите эти числа в порядке убывания их значений (начиная с самого большого): 0,8 0,65 0,6.
Ответ ребенка: 0,65 0,8 0,6
Ребенок прочел эти числа как 65, 8 и 6, поэтому поставил 65 на первое место. Один из способов обойти эту проблему, имея дело с десятичными дробями, состоит в том, чтобы поставить цифры в столбцы, а пустые места заполнить нулями:

Это естественным образом свяжет десятичные дроби с идеей разрядных значений цифр (десяток, сотен и тысяч), и сравнить десятичные дроби будет намного легче.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


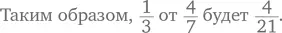
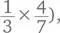 выглядит так:
выглядит так: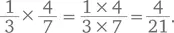
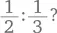

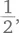 а закончили
а закончили 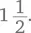 Реакция большинства людей на этот пример была бы приблизительно такой: «Ну вот, посмотрите, что получается. С этого момента математика перестает опираться на здравый смысл».
Реакция большинства людей на этот пример была бы приблизительно такой: «Ну вот, посмотрите, что получается. С этого момента математика перестает опираться на здравый смысл».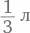 молока (не думайте о других ингредиентах – яйцах, муке и пр.). Сколько таких порций теста вы сможете изготовить из целого литра молока? Три.
молока (не думайте о других ингредиентах – яйцах, муке и пр.). Сколько таких порций теста вы сможете изготовить из целого литра молока? Три.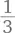 литра входит в литр трижды. Точно так же, как именно благодаря делению
литра входит в литр трижды. Точно так же, как именно благодаря делению 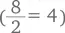 вы знаете, что «2 укладывается в 8 четыре раза», тот факт, что
вы знаете, что «2 укладывается в 8 четыре раза», тот факт, что 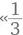 литра входит в литр трижды», тоже становится очевиден в результате деления:
литра входит в литр трижды», тоже становится очевиден в результате деления: 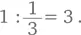
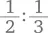 становится понятнее:
становится понятнее:
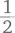 или
или 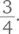 Отчасти это объясняется тем, что они иначе выглядят: действительно, 0,5 или 50 % совсем не похоже на
Отчасти это объясняется тем, что они иначе выглядят: действительно, 0,5 или 50 % совсем не похоже на 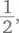 но смысл во всех трех записях содержится совершенно одинаковый. Зачем же тогда запутывать ситуацию и придумывать разные способы обозначения? Если все это просто
но смысл во всех трех записях содержится совершенно одинаковый. Зачем же тогда запутывать ситуацию и придумывать разные способы обозначения? Если все это просто 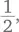 то почему всегда так и не писать? Причина в том, что десятичные дроби намного проще сравнивать и удобнее проводить с ними расчеты. Помните, как трудно было сравнивать
то почему всегда так и не писать? Причина в том, что десятичные дроби намного проще сравнивать и удобнее проводить с ними расчеты. Помните, как трудно было сравнивать 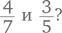 Так вот, если прибегнуть к помощи десятичных дробей и процентов, процедура сравнения стала бы намного проще.
Так вот, если прибегнуть к помощи десятичных дробей и процентов, процедура сравнения стала бы намного проще.







![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



