Делимость на 9. Сложите все цифры числа. Если получившаяся сумма кратна девяти, и только в этом случае, число без остатка делится на девять. Таким образом, 442 не делится на девять (сумма его цифр равна десяти), а 378 – делится (сумма цифр равна 18).
Проверьте себя
21. Признаки делимости
Сможете ли вы сказать, не производя вычислений, в каких из этих примеров деление выполняется без остатка?
1) 28 734: 2
2) 9817: 5
3) 183: 3
4) 4837: 9
5) 28 316: 6
Деление уголком – стандартный метод
Кто-то однажды сказал: «Всякий, кто в своей жизни решил уголком хотя бы два примера на деление, один из них решил напрасно».
Не исключено, что вам захочется вспомнить о ситуации, в которой вы в последний раз делили уголком (за исключением тех случаев, когда вы помогали ребенку справиться с домашним заданием). Австралия исключила это действие из своих учебных программ много лет назад, и никто, кажется, от этого не пострадал. В Великобритании кое-кто до сих пор рассматривает деление уголком как основу математики в начальной школе, так что, скорее всего, дети будут еще некоторое время этим заниматься. Напомним классический способ деления уголком [5].
517: 24. Здесь 517 – делимое, а 24 – делитель.

Мы не будем здесь рассказывать подробнее о делении уголком. Почему? Если вы уверенно владеете этим методом, то приведенного примера вам будет достаточно, чтобы все вспомнить, а если нет – лучше начать с нуля, используя методы, позволяющие разобраться, как это работает.
Деление на однозначное число
В тех случаях, когда делитель мал, процедура целиком не нужна. Поэтому для расчета 749: 7, можно использовать сокращенный вариант алгоритма (кстати говоря, в настоящее время его иногда называют методом автобусной остановки, поскольку форма записи здесь напоминает очередь из цифр в ожидании автобуса).
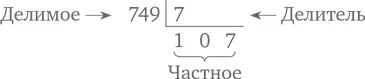
«Сценарий», которому учили многих из нас, выглядит примерно так:
• Семь укладывается в семь один раз, записываем 1 – первую цифру частного.
• Семь не укладывается в четыре, записываем это (пишем 0), переносим четыре.
• Семь укладывается в 49 ровно семь раз, пишем 7.
Ответ: 107.
В голове ребенка: объясняем неверные ответы
Вот как можно представить приведенный выше пример на простое деление в виде задачи. «Элинор хотела разрезать кусок ленты длиной 749 см на семь равных кусков. Какой длины оказался бы при этом каждый кусок?»
А вот ответы двух детей. Сможете ли вы понять, почему они сделали ошибки?

А.Ребенок сказал себе что-то вроде: «Семь делим на семь, получается один ровно, пишем 1. Дальше, семь в четыре не укладывается, писать нечего [на самом деле на этом этапе следовало написать 0]. Семь укладывается в 49 семь раз, пишем 7. Ответ: 17».
Б.Здесь мысленный «сценарий», вероятно, выглядел приблизительно так: «Семь укладывается в семь один раз, пишем 1. Семь в четыре не укладывается, записываем это, то есть пишем 0. Семь в девять укладывается один раз, остаток два, пишем 1 и остаток. Ответ: 101, остаток два».
Неверные сценарии детей не так уж далеки от правильного хода решения. Несложно ошибиться и вместо «Записываем, что не укладывается, то есть пишем 0» сказать себе что-то вроде: «Не укладывается, и писать здесь нечего», – или написать 0 и перейти к следующей цифре 9, считая, что четыре больше не требует никаких действий (в конце концов, с первой цифрой 7, после того как написали единицу, больше ничего не делали).
Одна из наших рекомендаций, которую мы то и дело повторяем, гласит, что детям, чтобы не делать ошибок в арифметике, важно думать о числах , а не о цифрах. Здесь вы видите, что в сценариях, в которых речь идет о цифрах, очень легко запутаться.
Деление кусками, или метод группировки
Взгляните, как ребенок может решать пример 749: 7, если учитель предлагает ученикам разобраться в том, как работает деление.
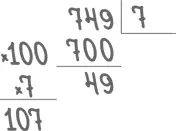
Что здесь происходит? Точно так же, как процесс умножения можно расписать подробнее, в расширенной форме, здесь ребенок использует расширенную форму для выполнения деления. При этом он говорит себе примерно следующее:
Читать дальше
Конец ознакомительного отрывка
Купить книгу


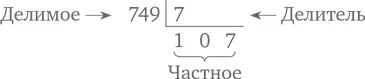

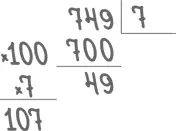







![Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]](/books/406847/rob-istuej-matematika-na-hodu-bolee-100-matematich-thumb.webp)



