Роб Истуэй - Математика для мам и пап - Домашка без мучений

Возьмем, 134 × 46. Можно решить этот пример так:

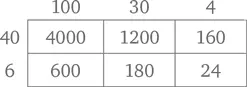
Если есть желание, так можно перемножать и тысячи, и более крупные числа. Хотя к тому моменту, когда ваш ребенок станет заниматься такими сложными расчетами, он почти наверняка будет уже знаком с традиционным методом умножения в столбик.

Книга стоит £9,47, и школа заказывает 62 экземпляра. Пользуясь методом решетки, найдите общую стоимость заказа.

У метода решетки есть еще одно достоинство, весьма важное, хотя и не существенное для учащихся начальной школы. Вероятно, вы помните, как во времена вашего детства математика в средней школе плавно переходила в алгебру и числа все чаще заменялись буквами. В частности, начинали появляться такие выражения, как (a + b) умножить на (c + d).

Что получится, если перемножить и раскрыть скобки? Многие родители при виде подобного застывают в страхе, пока не поймут, что это в точности та же процедура, что используется при перемножении чисел методом решетки. Представьте, что (a + b) умножить на (c + d) – это то же, что (20 + 4) умножить на (30 + 6), и вообразите, что вписываете эти числа в решетку и складываете результаты.

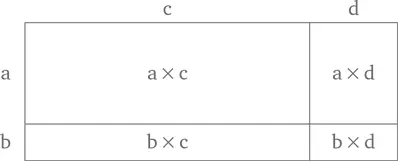
Все выглядит в точности так, как было бы с числами:

Поэтому ответ таков: a c + a d + b c + b d. Метод решетки представляет собой намного более удачное основание для изучения алгебры, чем метод умножения столбиком. Просто чтоб вы знали…

Деление часто оказывается для ребенка самой сложной из основных математических операций. Язык здесь может быть еще более непонятным, чем при умножении: «три в два не укладывается», «делим на», «остаток переходит». Насколько важно в целом деление столбиком, и почему оно вызывает у всех такие проблемы? Кроме того, если деление все уменьшает, то почему деление на 0,5 на калькуляторе дает в качестве ответа большее число?

1. Дети не до конца осознают, что деление – действие, обратное умножению, и потому не используют известные им факты умножения для получения соответствующих фактов деления. К примеру, если вы знаете, что 7 × 4 = 28, вы знаете также, что 28: 7 = 4 и 28: 4 = 7.

2. Считают, что при «делении» речь идет исключительно о том, что кто-то с кем-то «делится» («поделите 42 яблока на шесть человек»), но не о многократном вычитании («разложите 42 яблока в пакеты по семь яблок в каждом»).

3. Уверены, что деление все уменьшает. Но если поделить 35 конфет между пятью детьми, у каждого окажется по семь конфет, однако всего конфет по-прежнему будет 35. Конфеты никуда не пропали, их просто перераспределили.

Деление обычно представляют детям как идею о равном распределении. Особенно их увлекает идея раздачи конфет (и каждый хочет быть уверенным в том, что получит свою справедливую долю). Поэтому, если речь идет о примере 48: 8, то, как правило, он представляется в виде «реальной» задачки: «У меня есть 48 ирисок, и я хочу разложить их поровну в восемь пакетиков. Сколько конфет я положу в каждый пакетик?»

Но существует и другой способ интерпретации честного раздела. Сравните предыдущую задачку с этой: «У меня есть 48 ирисок. Я хочу разложить их в пакетики по восемь штук в каждом. Сколько пакетиков у меня получится?»

Эту задачу тоже можно решить, разделив 48 на восемь.

Между двумя этими задачами есть серьезное различие. В первом случае, в задаче с распределением, мы знаем, сколько у нас ирисок и в сколько пакетиков мы их хотим разложить. Чего мы не знаем, так это того, сколько ирисок в конце концов окажется в каждом пакетике. Чтобы решить эту задачу практически, вам пришлось бы в буквальном смысле распределять 48 объектов: обозначить как-то восемь пакетиков и раскладывать: «Одну тебе, одну тебе…», – пока ириски не закончатся.

Во второй задаче ситуация немного иная. У вас по-прежнему имеется 48 ирисок; на этот раз вы знаете, сколько ирисок вы хотите положить в каждый пакетик, зато не знаете, сколько получится пакетиков. Чтобы решить эту задачу практически, вам пришлось бы выложить кучкой 48 объектов, а затем взять из кучки восемь конфет и положить их в первый пакетик, еще восемь положить во второй и т. д., пока все ириски в кучке не закончились бы. Здесь деление – это скорее повторяемое вычитание, чем распределение.