Роб Истуэй - Математика для мам и пап - Домашка без мучений

Отсюда очевидно, что 3 × 14 – то же самое, что 3 × 10 плюс 3 × 4, или 30 + 12.

Вместо того чтобы вырисовывать каждую точку (что, кстати, может подтолкнуть ребенка к простому их пересчету), далее детям рекомендуют представлять массивы точек в виде прямоугольников, а числом точек подписывать верхние и боковые стороны этих прямоугольников.

3 × 14 превращается в следующее:

Обратите внимание: прямоугольники рисуются не в масштабе – в этом нет нужды. Мы просто чертим прямоугольники, в которые можно вписать ответы, приблизительно так:

Иными словами, 3 × (10 + 4) = 30 + 12 = 42.

Более сложные примеры можно решать аналогичным способом. 24 × 36 возможно представить так:

Этот большой прямоугольник разбиваем на части, представляющие десятки и единицы…

Получается нечто, напоминающее решетку, – именно поэтому такой метод называют методом решетки. Теперь, чтобы найти 36 × 24, нужно сложить число точек, которые уместились бы в каждой секции решетки.

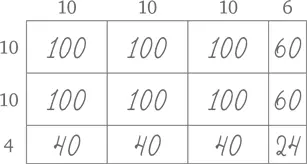
Сложите шесть раз по 100, два раза по 60, три раза по 40 и 24 – и получите ответ 864. Прием может показаться нудным и длинным (он такой и есть!), но применять его быстрее, чем пересчитывать все точки поштучно. Кроме того он дает возможность понять, что, собственно, происходит.

Решите пример 23 × 13, нарисовав решетку и представив числа как десятки и единицы.

Многие дети быстро соображают, что можно сэкономить время, если блоки сделать побольше . Намного проще разбить 24 × 36 так:

Теперь нам нужно выполнить всего четыре действия:

Ответ находится путем сложения результатов действий во всех четырех ячейках решетки или: 600 + 120 + 120 + 24.

Если ребенок уже уверенно пользуется методом решетки, ему остается сделать всего один небольшой шаг – и вообще перестать тратить время на чертеж. Вместо этого он записывает то, что раньше помещалось в решетке, в виде четырех отдельных примеров:

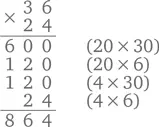
Это уже очень близко к традиционному методу умножения столбиком, и детям, которые чувствуют себя уверенно, можно показать, как сделать последний шажок и перейти к компактному варианту записи (см. «Сложение столбиком: стандартный метод» в главе «Сложение и вычитание: письменные методы»).

Но зачем двигаться к этому таким кружным путем? Причина в том, что не все дети добираются до умножения в столбик в его традиционной форме. Тем, кому плохо дается умножение, метод решетки гарантирует алгоритм, который они способны понять. И если ребенок на любом этапе вычислений что-то забывает или начинает путаться, он может «отступить» и прибегнуть к предыдущему методу, чтобы восполнить недостающее. Так что нельзя сказать, что от детей теперь не требуют умения умножать в столбик. Скорее цель в том, чтобы движение к этому происходило поэтапно, поскольку понимание в данном случае не менее важно, чем владение методом.

Как определить, не решая примеры до конца, что эти ответы ошибочны?

1) 37 × 46 = 1831

2) 72 × 31 = 2072

3) 847 × 92 = 102 714

Метод решетки можно применять для перемножения не только двузначных, но и вообще любых чисел – хотя, разумеется, с увеличением чисел процесс становится более сложным.