Роб Истуэй - Математика для мам и пап - Домашка без мучений

Вот только… 12 то и дело всплывает в расчетах: множество людей по-прежнему меряет и считает в дюймах (в Америке это стандарт), а яйца и сегодня продают дюжинами и полудюжинами.

Мало того. У ребенка, свободно перемножающего числа больше десяти, начинает вырабатываться понимание того, как перемножаются большие числа. Знание таблиц умножения на 11 и 12 помогает заметить интересные закономерности, которые вы вполне могли бы пропустить, если бы остановились на десяти. Приведем полную таблицу умножения до 12.

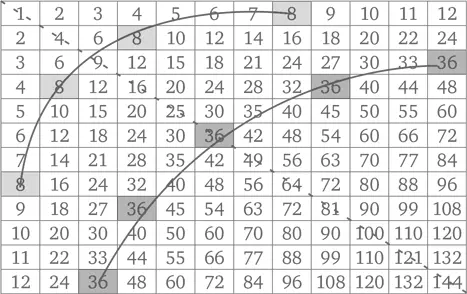
Обратите внимание: число восемь, к примеру, встречается в таблице четыре раза, тогда как 36 – пять раз. Если соединить все ячейки с числом восемь, получится плавная кривая . То же можно сказать и про ячейки с числом 36. В самом деле, если какое-то число появляется в таблице больше двух раз, то все места его появления можно соединить плавной кривой примерно одинаковой формы – и если нарисовать на одной таблице все такие кривые, то они ни разу не пересекутся между собой. (Кривую такой формы называют гиперболой.)

Вы можете подтолкнуть своего ребенка к самостоятельному исследованию, которое займет его (может быть) на полчаса, а то и больше. Распечатайте несколько экземпляров таблицы умножения двенадцати первых чисел на 12, а затем попросите его сделать следующее:

• раскрасить все ячейки с четными числами красным цветом, а с нечетными – синим;

• определить, какие числа встречаются там чаще всего;

• сказать, сколько в таблице встречается различных чисел;

• ответить на вопросы: «Какое самое маленькое число не встречается в этой таблице? Какие еще числа от 1 до 100 в ней отсутствуют?»

Таблица умножения на 11 строится проще всего.

1 × 11 = 11

2 × 11 = 22

3 × 11 = 33

4 × 11 = 44

5 × 11 = 55

6 × 11 = 66

7 × 11 = 77

8 × 11 = 88

9 × 11 = 99

Но что же дальше? Есть очень симпатичный простой прием, позволяющий без труда умножить любое число от 10 до 99 на 11:

• Возьмите любое число от десяти до 99 – пусть это будет, скажем, 26.

• Разбейте его на два числа и раздвиньте их, чтобы в середине образовался пробел: 2 _ 6.

• Сложите между собой две цифры вашего числа. 2 + 6 = 8 и вставьте то, что получилось, в середину: 2 8 6

Это ответ! 26 × 11 = 286.

Но будьте осторожны. Что получится, если вы перемножите 75 × 11?

• Разбиваем число: 7 _ 5

• Складываем: 7 + 5 = 12

• Вставляем результат в середину и получаем 7125, что очевидно неверно!

В чем дело? В этом примере есть небольшая хитрость, которую нужно применять тогда, когда цифры, использующиеся для обозначения числа, в сумме дают десять или больше (7 + 5 = 12). Прибавляем один к первой из наших цифр. Следовательно, 75 × 11 будет не 7125, а (7 + 1)25, или 825. Так что фокус на самом деле не так прост, как может показаться.

Решите в уме:

1) 33 × 11

2) 11 × 62

3) 47 × 11

Цель этой игры – развить навык быстрого пользования таблицей умножения. Вам потребуется колода игральных карт без картинок и калькулятор. Решите, кто из играющих первым будет использовать калькулятор.Правила:

• Игрок с калькулятором должен перемножить два выпавших на картах числа; при этом он должен использовать калькулятор, даже если знает ответ (да, это может быть очень тяжело).

• Другой играющий должен перемножить те же два числа в уме.

• Тому, кто получает ответ первым, достается очко.

• После десяти попыток игроки меняются местами.

Овладев таблицей умножения и прочно включив ее в свой математический арсенал, дети начинают двигаться дальше и изучать методы и стратегии умножения и деления более крупных чисел. Как мы видели, письменные методы, которые преподают сегодня в школе, довольно сильно отличаются от тех, что преподавали учащимся еще несколько лет назад. Если дети умудряются ошибаться даже при сложении и вычитании на бумаге, то вероятность ошибок в длинных примерах на умножение и деление оказывается еще выше. Одна из причин состоит в том, что они приступают к умножению длинных чисел сразу после решения множества задач на сложение и вычитание таких чисел. А поскольку те и другие примеры оформляются сходным образом, дети часто начинают применять к умножению правила, уже усвоенные ими применительно к сложению: как ни печально, получить при этом верный ответ удается не всегда. Поэтому не спешите с умножением и делением – не исключено, что вашему ребенку кажется, будто он понимает, что происходит, хотя на самом деле это не так.