Роб Истуэй - Математика для мам и пап - Домашка без мучений

Помогая ребенку выучить таблицу умножения, очень важно объяснить ему, что порядок чисел не имеет значения: 3 × 7 дает тот же ответ, что и 7 × 3. Математикам эта мысль так нравится, что они придумали для нее особое название: коммутативныйзакон.

Взрослым серьезнейшая идея о том, что умножению свойственна коммутативность, обычно кажется самоочевидной. С детьми все по-другому. Нужно немало времени, чтобы эта идея закрепилась в сознании мальчика или девочки, – ведь при знакомстве с умножением это его качество, как правило, явно не проявляется. Если у Джо есть три пакетика с конфетами, в каждом из которых лежит по семь конфет, а у Сэма – семь пакетиков с тремя конфетами в каждом, не слишком очевидно, что у Джо ровно столько же конфет, сколько и у Сэма. (Если предложить маленькому ребенку два этих варианта, он с большой вероятностью выберет семь пакетиков в надежде получить больше конфет.)

Один из лучших способов наглядно показать ребенку, почему 3 × 7 равно 7 × 3, заключается в использовании массива. «Массив» – слово, которого вы, вероятно, не встречали в курсе школьной математики, но сегодня оно прочно вошло в соответствующий лексикон и активно используется. Это специальное математическое слово, обозначающее набор чисел или фигур, заключенный в прямоугольник. Вот, к примеру, массив из трех строк и семи столбцов.

Массив – чрезвычайно важное понятие, это простое и визуальное средство помочь ребенку разобраться в том, как работают умножение и дроби. Сколько всего точек в прямоугольнике 3 на 7? Три строки по семь элементов насчитывают 21 элемент. Иными словами, массивы – доступный для понимания способ наглядно представить умножение, в данном случае 3 × 7 = 21.

Что, если мы нарисуем массив двумя разными способами?

Первый массив показывает 3 × 7, второй 7 × 3. (Традиционно эти схемы «читаются» в таком порядке: строки, затем столбцы.) Очевидно, что в обоих массивах должно быть одинаковое число точек (их не обязательно при этом считать поштучно), поскольку, если первый массив повернуть на четверть оборота, он будет выглядеть в точности как второй. Иными словами, 3 × 7 = 7 × 3.

И в самом деле, каким бы ни был массив (или какие бы числа вы ни перемножали), ответ будет один и тот же, с какой стороны ни посмотри. 247 × 196 – то же самое, что 196 × 247, и чтобы в этом убедиться, достаточно вспомнить о массивах.

Оглядитесь, поищите рядом, в доме или на улице, какие-нибудь массивы. Покажите их своему ребенку, поговорите о них. Взгляните, к примеру, на пластиковый подносик с пирожными в коробке. Пирожные на нем уложены в массив 4 на 3. А если повернуть? Тогда 3 на 4. А теперь взгляните на окна многоэтажки. Вот это да, это тоже массив, 5 на 4! А может быть, 4 на 5, как посмотреть? Этого мало. Стоит начать обращать внимание на массивы, как выяснится, что они всюду.

Если вы уже усвоили с детьми идею о том, что 3 × 7 – это то же самое, что 7 × 3, то число фактов умножения, которые вам необходимо запомнить, резко уменьшается. Стоит заучить 3 × 7 – и в качестве бонуса вы получаете ответ на 7 × 3. Это, по существу, математический эквивалент рекламного приема «купи один, второй получи бесплатно». Знание этого переместительного закона снижает число фактов умножения со 100 до 55 (не ровно наполовину из-за случаев возведения в квадрат, таких как 3 × 3 или 7 × 7, которые не имеют пары).

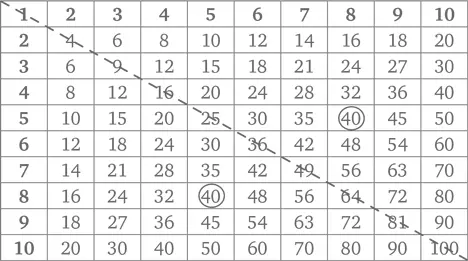
Можно увидеть, как происходит это снижение, если еще раз посмотреть на 100 чисел в таблице умножения на 10, приведенной ранее.

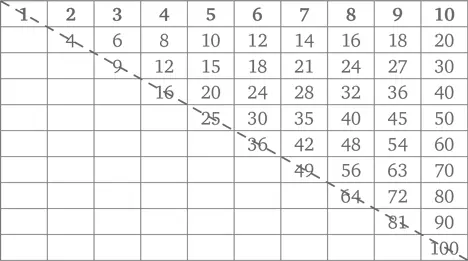
Каждое из чисел, расположенных выше пунктирной диагонали (к примеру, 5 × 8 = 40), присутствует и ниже нее (8 × 5 = 40). Пунктирная диагональная линия является также линией симметрии. (Обратили внимание, какие числа стоят на пунктирной линии? См. ниже.)

Дети обычно начинают учить таблицу умножения при помощи счетных алгоритмов. Чтобы сообразить, чему равно 8 × 4, они считают так: 4, 8, 12, 16, 20, 24, 28, 32. Но если ты знаешь, что восемью четыре – то же самое, что четырежды восемь, то 8, 16, 24, 32 будет быстрее. В Японии детей специально учат «ставить меньшее число первым». Семь раз по 3? Не делайте так, считайте лучше 3 раза по 7.