2.1.7.Основанная на линейном анализе устойчивости методика поиска устойчивых состояний является общей для систем, имеющих различную природу. Чтобы подчеркнуть это обстоятельство, в разделе 2.3 рассмотрена задача, в которой так же осуществлен поиск асимптотически устойчивого стационарного состояния (т. е. аттрактора, см. раздел П5.6), но теперь уже в физической системе – генераторе Ван дер Поля. Генератор Ван дер Поля представляет собой колебательную систему с нелинейными свойствами и часто используется в теоретических исследованиях, связанных с электроникой. Как показано в разделе 2.3, в пространстве двух переменных устойчивым стационарным состоянием генератора является предельный цикл.
2.2. Математическая модель устойчивости страховой фирмы
На примере предприятия, занимающегося конкретной деятельностью, мы продемонстрируем возможности линейного анализа устойчивости для математического моделирования экономической системы.
Поставим перед собой задачу определить устойчивые состояния страховой фирмы, а также экономические показатели, от которых зависит устойчивость такой фирмы [5, 30].
Важнейшей целевой функцией любой фирмы является прибыль. Согласно классическому определению, прибыль ( Y ) представляет собой разность между доходом ( D ) и расходом ( R ): Y = D – R . Специфика страховой фирмы проявляется в составляющих ее дохода и расхода. Введем следующие обозначения:
N – количество клиентов;
s – страховой взнос клиента;
p – размер страховой выплаты клиенту;
Q * – количество страховых выплат.
Тогда доход фирмы равен sN , а расход – pQ *. В результате приходим к известному уравнению, характеризующему суть страхового бизнеса:
Y = sN – pQ*. (21)
2.2.1. Модель государственной страховой фирмы
Характерной особенностью государственной страховой фирмы является требование всеобщего страхования (например, в рамках конкретного страхового профиля), т. е. N = const .
В качестве переменной задачи выберем прибыль страховой компании Y . Сформулируем главную пропорцию: прирост прибыли dY/dt (увеличение прибыли с течением времени t ) пропорционален числу клиентов, а также величине самой прибыли, если часть прибыли вкладывается в какие-нибудь доходные предприятия (~ NY ). Кроме того, следует отнять ту часть прироста прибыли, которую фирма не дополучила из-за выплат клиентам (~ Q *). Уравнение, соответствующее данной пропорции, примет вид
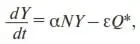 (22)
(22)
где знак пропорции ~ мы заменили коэффициентами пропорциональности α и ε .
Выразим Q * из (21)
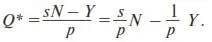
Подставив это выражение в (22), получим
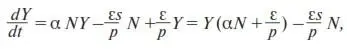
и окончательно
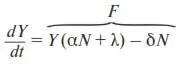 (23)
(23)
– эволюционное уравнение государственной страховой фирмы . В (23) введены обозначения: λ = ε/p; δ = εs/p .
Стационарное решение Y стуравнения (23) найдем из условия (П8) ( dY ст/ dt = 0):
0 = Y cт(α N + λ ),
откуда
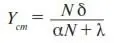
– стационарное значение прибыли в государственной страховой фирме.
Зададим возмущение y для Y ст. Поскольку в задаче только одна переменная, а именно Y (прибыль), то закон изменения возмущения с течением времени (П13) запишется в простом виде
y = c exp (ωt).
Характеристическое уравнение (П14) также сильно упрощается:
a 11– ω = 0,
Следовательно, ω = a 11 и
y = c exp (a 11t). (24)
где a 11вычисляется по формуле (П12). В этой формуле перейдем к обозначениям без индексов, так для одной переменной в них нет смысла:
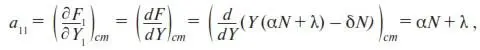 (25)
(25)
где F – правая часть эволюционного уравнения (23). Все величины в (25) положительные (в частности, из (22) видно, что прибыль фирмы будет увеличиваться, т. е. dY/dt > 0 , если коэффициент пропорциональности α положителен). Следовательно,
Читать дальше

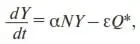 (22)
(22)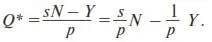
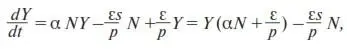
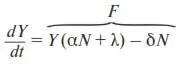 (23)
(23)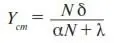
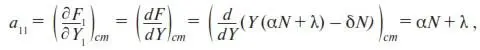 (25)
(25)









