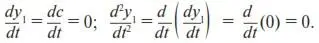
Найденное значение с подставим в (13):
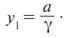
– частное решение уравнения (5). Его общее решение запишем по формуле (6) ( y * возьмем из (9)):
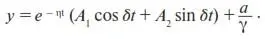 (14)
(14)
Выражение в скобках можно упростить, заменив постоянные A 1и A 2на новые постоянные A и φ 0по формулам
A 1= A sin φ 0и A 2= A cos φ 0
(легко увидеть, что 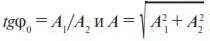 ). Тогда
). Тогда
A 1cos δt + A 2sin δt = A (sin φ 0cos δt + cos φ 0sin δt) = A sin (δt + φ 0).
В результате (14) примет вид
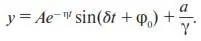 (15)
(15)
Уравнение (15) представляет собой формулу зависимости от времени количества товара, приобретаемого благодаря действию рекламы.
Из (15) следует, что если рекламировать товар с постоянной интенсивностью достаточно долго ( a = const ), то начнутся колебания y вокруг постоянного значения a/γ , т. е. возникнет чередование периодов положительного и отрицательного восприятия рекламы (см. рис. 1).
Сравним (15) с известным законом колебательного движения
x = A sin (ωt + φ 0).
Как видим, δ совпадает по смыслу с циклической частотой ω . Отсюда, воспользовавшись соотношением для периода колебаний T = 2π/ω , получаем формулу для промежутка времени положительного восприятия рекламы:
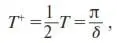
где δ вычисляется из (8). Для определения численных значений коэффициентов, входящих в (8), возможно использование эконометрических методов.
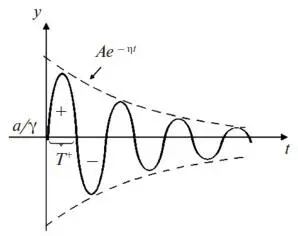
Рис. 1.Чередование периодов положительного и отрицательного восприятия рекламы
Глава 2
Приложение дифференциального исчисления для анализа устойчивости систем
К настоящему времени в экономике системные закономерности наиболее подробно рассмотрены в математических моделях экономического роста крупных регионов, например городов, областей, государств (см., например, [7,14]). При этом в качестве переменных величин, как правило, выбирались национальный доход, капитал, средний уровень зарплаты, цены и т. п. Модели таких систем характеризуют результаты согласованного поведения большого количества фирм, входящих в регион. В данной главе будет проведен анализ поведения отдельной фирмы, для которой экономика региона играет роль внешней среды.
Мы рассмотрим фирму, обладающую следующими средними (по региону) показателями: числом сотрудников и величиной оборотного капитала. Главная задача данного раздела – раскрыть важную роль управляющих параметров, которую они играют при выборе системой пути к тому или иному устойчивому состоянию.
Вначале мы построим общую математическую модель поведения средней фирмы. Затем в качестве примера найдем устойчивые состояния предприятия, занимающегося конкретным видом деятельности, например страхованием.
2.1. Анализ устойчивости фирмы, средней (в некотором регионе) по числу сотрудников и оборотному капиталу
(Изложение данного раздела следует работам [26, 28].) Пусть в фирме работает Y 1сотрудников, а ее капитал, выраженный в некоторых условных единицах, равняется Y 2. Необходимо определить, возможно ли в такой системе устойчивое состояние и какому типу устойчивости оно соответствует?
Поиск устойчивых стационарных состояний проведем с помощью линейного анализа устойчивости. Для этого воспользуемся его схемой (см. Приложение П2.2).
2.1.1.Начнем с составления эволюционного уравнения. Левая часть эволюционного уравнения представляет собой производные первого порядка от величин, принятых в качестве переменных (см. (П6) 3). В нашем случае речь идет о Y 1и Y 2:
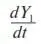 – скорость роста числа сотрудников;
– скорость роста числа сотрудников;
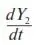 – скорость увеличения капитала фирмы.
– скорость увеличения капитала фирмы.
Читать дальше

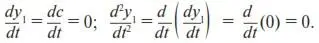
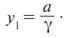
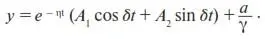 (14)
(14)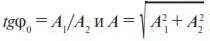 ). Тогда
). Тогда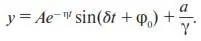 (15)
(15)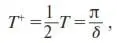

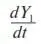 – скорость роста числа сотрудников;
– скорость роста числа сотрудников;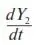 – скорость увеличения капитала фирмы.
– скорость увеличения капитала фирмы.









