Сформулируем первую главную пропорцию 4:
скорость роста числа сотрудников ( dY 1/ dt ) пропорциональна числу новых сотрудников минус ту ее часть, которая связана с количеством уволившихся.
При этом количество новых сотрудников пропорционально капиталу фирмы (~ Y 2, так как в среднем люди предпочитают работать в более богатой фирме), а количество уволившихся составляет некоторую долю от числа имеющихся (~ Y 1). Заменяя знаки пропорции (~) на коэффициенты пропорциональности, первую главную пропорцию приводим к следующему уравнению:
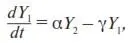 (16)
(16)
где α – коэффициент пропорциональности, показывающий, какую часть своего капитала может выделить фирма, чтобы привлечь новых сотрудников; γ – коэффициент пропорциональности, обобщающий в себе различные причины, в результате которых сотрудник может уволиться (или его уволят).
Cформулируем вторую главную пропорцию:
скорость увеличения капитала пропорциональна прибыли от вложения капитала минус расходы на сотрудников.
При этом прибыль от вложения капитала пропорциональна величине вложенного капитала (~ Y 2), а расходы на сотрудников пропорциональны их количеству (~ Y 1). Так же заменяя знаки пропорции (~) на коэффициенты пропорциональности, вторую главную пропорцию приводим к уравнению:
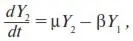 (17)
(17)
где µ – коэффициент пропорциональности, показывающий эффективность работы фирмы на рынке; β – коэффициент пропорциональности, обобщающий в себе среднюю величину затрат фирмы на одного сотрудника.
2.1.2.Эволюционным уравнением задачи является система уравнений (16) и (17), так как она удовлетворяет общему виду (П6) эволюционных уравнений:
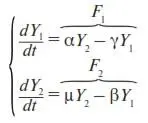
Применив к (18) условие (П8), найдем стационарное решение:
Y 1ст= Y 2ст= 0. (19)
2.1.3.Обратите внимание: наша модель средней фирмы имеет две переменные Y 1и Y 2. Следовательно, мы можем воспользоваться результатами Приложения П2.3, полученными для системы, так же с двумя переменными. В частности, чтобы проверить стационарное решение (19) на устойчивость, достаточно определить соотношение знаков у величин B , ∆ и D . Последние вычисляются по формулам (П22). В эти формулы входят четыре коэффициента линейного разложения: a 11, a 12, a 21и a 22. Их мы найдем с помощью (П12), в которой F i возьмем из системы эволюционных уравнений (18) нашей задачи.
Итак, согласно (П12),
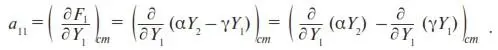
В первом слагаемом берется частная производная по переменной Y 1от выражения αY 2, которое, как видим, не содержит Y 1, поэтому, согласно правилу вычисления частной производной, это выражение считается постоянным и производная от нее равна нулю. Во втором слагаемом производная берется от выражения γY 1, которое считаться постоянным не может, так как содержит Y 1. Поэтому дальнейшие вычисления для a 11примут вид
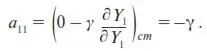
Аналогично рассуждая, находим остальные коэффициенты линейного разложения:
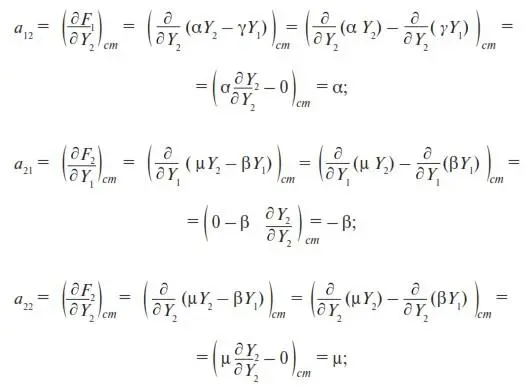
Подставив найденные значения a 11, a 12, a 21, и a 22в (П22), получим
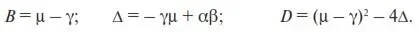 (20)
(20)
2.1.4.Для средней фирмы коэффициенты α и β должны быть сравнительно большими, так как оба относятся к расходам на сотрудников, а коэффициент µ и γ , наоборот, не должен быть большими потому, что, во-первых (в случае µ ), у средней фирмы прибыль от операций на рынке не является слишком высокой, иначе бы фирма была богатой, а не средней; и во-вторых (в случае γ ), в цивилизованном обществе в средней фирме текучесть кадров невелика.
С учетом сказанного из формул (20) можно точно определить знаки величин ∆ и D . Действительно,
Читать дальше

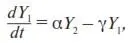 (16)
(16)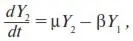 (17)
(17)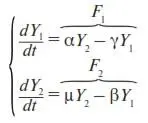
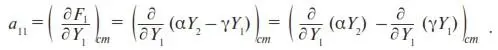
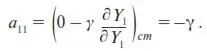
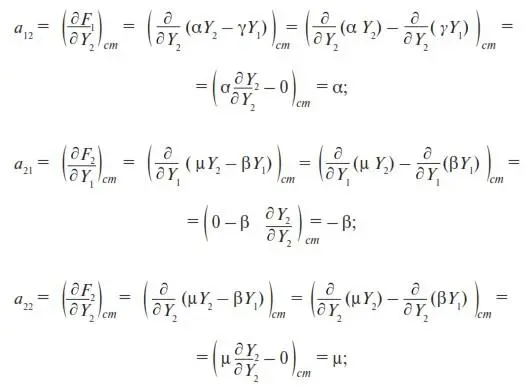
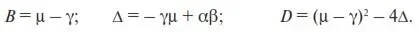 (20)
(20)









