a 11> 0.
Как видим, возмущение y из (24) увеличивается с течением времени. Последнее означает, что Y ст является неустойчивым.
Таким образом, в рамках рассмотренной модели стабильное получение прибыли государственной страховой фирмой возможно лишь в сильно консервативном обществе, когда возмущение, создаваемое конкуренцией на рынке, отсутствует.
2.2.2. Модель частной страховой фирмы
Характерной особенностью частной страховой фирмы является зависимость числа клиентов от времени. Следовательно, в этой модели число клиентов N необходимо учитывать в качестве переменной, которую обозначим как Y 1. Как и в предыдущем случае, прибыль страховой фирмы является переменной величиной, ее мы обозначим Y 2.
2.2.2.1.Главные пропорции частной страховой фирмы можно сформулировать следующим образом.
1. Прирост клиентов dY 1/dt пропорционален размеру получаемой прибыли Y 2(средний клиент предпочитают иметь дело с более богатой фирмой), среднему в данном регионе доходу клиента D 0и среднему в данном регионе количеству несчастных случаев Q ( ~Y 2D 0Q ). Отрицательная составляющая пропорции обусловлена теми клиентами, которые по каким-то причинам отказались от услуг фирмы (математически количество таких клиентов составляет некоторую долю от общего числа клиентов, которая статистически тем больше, чем больше у фирмы клиентов), т. е. отрицательная составляющая ~ Y 1.
2. Прирост прибыли dY 2/dt пропорционален числу клиентов Y 1, а также той части прибыли Y 2, которую фирма вкладывает в доходные предприятия ( ~Y 1Y 2 ). Отрицательная составляющая представляет собой часть прироста прибыли, которую фирма не дополучила из-за выплат клиентам (~ Q *).
Заменив знак пропорции ~ на коэффициенты пропорциональности α, γ, µ и β , придем к следующей системе двух уравнений
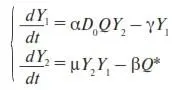
или
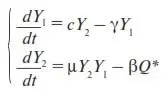
где c = αD 0Q.
Количество страховых выплат Q * найдем из (21) (напомним, что в данной модели в роли Y выступает Y 2, в роли N выступает Y 1):
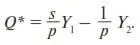
Подставим это выражение в (26)
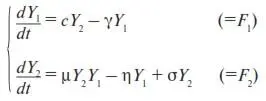 (27)
(27)
где введены обозначения σ = β/ p; η = βs/p .
Выражение (27) представляет собой систему эволюционных уравнений частной страховой фирмы (сравните с (П6)).
2.2.2.2.Найдем стационарное решение. Для этого к (27) применим условие (П8):
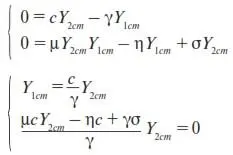
Как видим, второе уравнение дает для Y 2стдва значения:
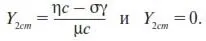
С учетом первого уравнения приходим к двум стационарным решениям (стационарным состояниям фирмы):
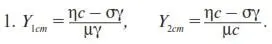 (28)
(28)
2. Y 1ст = Y 1ст = 0. (29)
2.2.2.3.Чтобы проверить данные стационарные решения на устойчивость, необходимо задать их возмущения. Затем следует проанализировать, как возмущения изменяются с течением времени: если уменьшаются, то состояние устойчиво, если увеличиваются, то неустойчиво.
Учтем, что наша модель содержит две переменные Y 1и Y 2. Благодаря этому процесс выяснения устойчивости упрощается. Мы можем воспользоваться результатами Приложения П2.3, полученными для системы с двумя переменными. В частности, чтобы проверить стационарные решения (28) и (29) на устойчивость, достаточно определить соотношение знаков у величин B , ∆ и D . Последние вычисляются по формулам (П22). В эти формулы входят четыре коэффициента линейного разложения: a 11, a 12, a 21и а 22. Их мы найдем с помощью (П12), в которой F i возьмем из системы эволюционных уравнений (27) нашей задачи.
Согласно (П12),
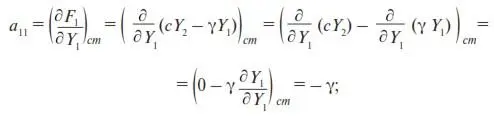 (30)
(30)
Читать дальше

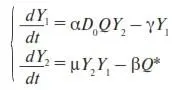
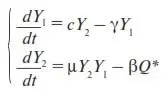
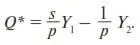
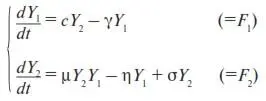 (27)
(27)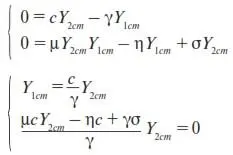
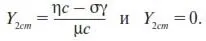
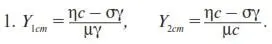 (28)
(28)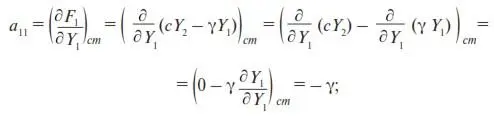 (30)
(30)









