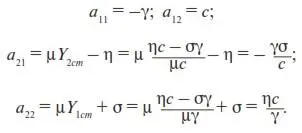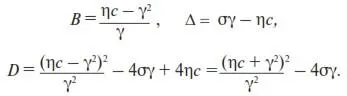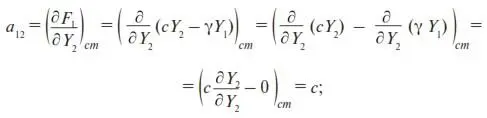 (31)
(31)
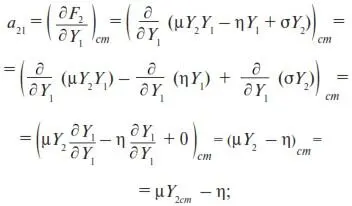 (32)
(32)
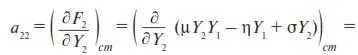
 (33)
(33)
1. Вначале проверим на устойчивость решение (28). Для этого его следует подставить в полученные выше выражения для а 21и а 22. В результате найдем
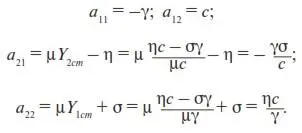
По формулам (П22) вычислим B , ∆ и D :
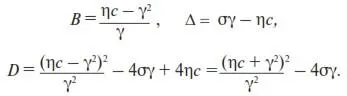
Чтобы определить их знаки, проведем сравнительную оценку величин коэффициентов γ, σ, η и с .
Коэффициент γ характеризует долю клиентов, решивших расторгнуть страховые отношения с данной фирмой (см. формулировку первой главной пропорции в 2.2.2.1). Если фирма не банкрот, то γ должна быть малой величиной.
Напомним, что σ = β/p , при этом p – размер страховой выплаты клиенту, т. е. большая величина. Поэтому мы полагаем σ малой величиной.
Так как η = s β/p , т. е. в s раз больше, чем σ, то η полагаем сравнительно большой величиной (напомним, что s >>1).
Величина c также должна быть большой, так как этот коэффициент пропорционален доходу D 0( D 0> 1) и количеству несчастных случаев Q за некоторый период ( Q >> 1).
В результате получаем следующее распределение знаков:
B > 0; ∆ < 0; D > 0.
Такое сочетание знаков совпадает с (П32). В этом случае стационарное решение (28) соответствует седловой неустойчивости.
Таким образом, решение (28) является неустойчивым.
2. Проверим на устойчивость стационарное состояние (29). Для этого его стационарные значения Y 1сти Y 2стподставим в (32) и (33). В результате с учетом (30) и (31) найдем:
a 11= – γ; a 12= c;
a 21= µY 2ст– η = 0 – η = – η;
a 22= µY 1ст+ σ = 0 + σ = σ.
По формулам (П22) вычислим B , ∆ и D :
B = σ – γ, ∆ = ηc – σγ, D = (σ + γ) 2– 4ηc.
Выше мы уже установили, что γ и σ меньше, чем η и с . Это позволяет нам определить знаки только величин ∆ и D : ∆ > 0; D < 0. Для B возникают две ситуации.
Ситуация 1: σ > γ . В этой ситуации большинство клиентов сохраняют верность фирме ( γ уменьшается). При этом распределение знаков имеет вид
B > 0; ∆ < 0; D > 0.
Последнее совпадает с (П30), т. е. в данном случае решение (29) соответствует неустойчивому фокусу (см. рис. П5). Расширяющаяся спираль указывает на рост значений переменных Y 1и Y 2(числа клиентов и прибыли).
Ситуация 2: σ < γ. Эта ситуация возникает, если фирма по каким-либо причинам теряет часть клиентов ( γ увеличивается). Распределение знаков имеет вид
B < 0; ∆ < 0; D > 0.
Данное сочетание знаков совпадает с (П25), т. е. в данном случае решение (29) соответствует устойчивому фокусу (см. рис. П2). Сжимающаяся спираль указывает на уменьшение числа клиентов Y 1и прибыли Y 2.
На практике механизм перехода фирмы из одной ситуации в другую может выглядеть следующим образом.
В ситуации 1 благодаря состоянию «неустойчивый фокус» (расширяющаяся спираль в пространстве координат Y 1и Y 2) происходит рост числа клиентов и прибыли. По мере роста числа клиентов увеличивается и число страховых выплат. Наступает момент, когда клиентов становится настолько много, что их взносы не покрывают убыток от страховых выплат. В этом случае фирма вынуждена уменьшить, например, размер страховой премии. Из-за этого часть клиентов уходит из данной фирмы ( γ увеличивается). В результате фирма оказывается в ситуации 2. Этой ситуации соответствует состояние «устойчивый фокус» (сжимающаяся спираль в пространстве координат Y 1и Y 2). В таком состоянии число клиентов уменьшается до тех пор, пока прибыль фирмы не позволит вернуться к прежней повышенной страховой премии. В этом случае клиенты перестанут уходить из фирмы, что соответствует уменьшению γ . В результате фирма переходит в ситуацию 1, и т. д.
2.2.2.4.Таким образом, мы показали, что система «частная страховая фирма» с течением времени приходит к устойчивому состоянию, представляющему собой колебания вокруг оптимальных значений числа клиентов и размера прибыли. Сами оптимальные значения зависят от величин коэффициентов γ, σ, η и с .
Читать дальше

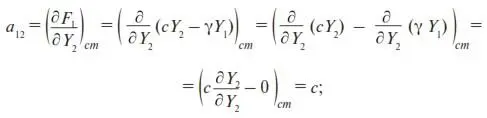 (31)
(31)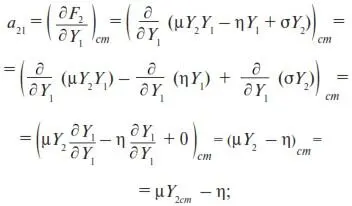 (32)
(32)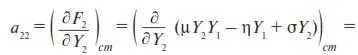
 (33)
(33)