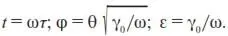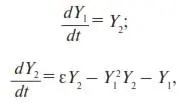2.3. Модель устойчивости физической системы: генератор Ван дер Поля
В этом разделе мы покажем, что устойчивое поведение маятника, колеблющегося в среде с переменной вязкостью, и устойчивое поведение средней фирмы, рассмотренное нами в разделе 2.1, имеют много общего [28].
2.3.1.Рассмотрим систему, представляющую собой математический маятник, совершающий колебания в вязкой среде, коэффициент вязкости γ которой зависит от θ – угла отклонения маятника от положения равновесия – по следующему закону: а) γ < 0 при малых θ и б) γ > 0 при больших θ . Такая система при некотором критическом значении угла θ должна совершать устойчивые колебания по типу предельного цикла (т. е. с постоянной амплитудой) [2].
Нетрудно сообразить, что указанному закону удовлетворяет следующее выражение
γ = γ 0(θ 2– 1),
где γ 0– коэффициент вязкости среды в отсутствие колебаний.
Подставив это выражение вместо коэффициента вязкости в известное уравнение колебаний маятника в вязкой среде (см., например, (П15)), получим
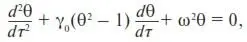 (34)
(34)
где τ – время; ω 2= gK – квадрат циклической частоты колебаний; K – кривизна траектории маятника; g – ускорение свободного падения.
Уравнение (34) называется уравнением Ван дер Поля , а система, которую оно описывает, – генератором Ван дер Поля [2].
В безразмерном виде уравнение (35) имеет вид:
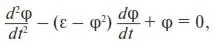 (35)
(35)
где 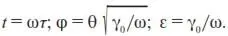
2.3.2.Покажем, что устойчивым стационарным состоянием (аттрактором) генератора Ван дер Поля действительно является предельный цикл. С этой целью уравнение (35) приведем к виду эволюционного уравнения (см. (П6)):
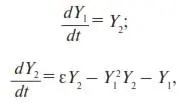
где Y 1= φ; Y 2= dφ/dt ;
F 1= Y 2;
F 2= εY 2– Y 1 2Y 2– Y 1. (36)
Находим стационарное решение
Y 1cm= Y 2ст= 0. (37)
По формуле (П12) с учетом (36) находим коэффициенты линейного разложения
а 11= 0;
а 12= 1;
а 21= –2Y 1стY 2ст– 1;
а 22= ε – Y 21ст.
По формулам (П22) находим
B = ε – Y 2 1ст;
∆ = 2Y 1стY 2ст+ 1; (38)
D = (ε – Y 2 1ст) 2– 4 ∆.
Подставив стационарное решение (37) в (38), получим, что
B > 0; ∆ > 0; D = ε 2– 4. (39)
2.3.3.Если ε достаточно мало, то D становится отрицательным, а распределение знаков в (39) соответствует неустойчивому фокусу (см. (П30)). В этом случае фазовая траектория в координатах Y 1и Y 2будет представлять собой спираль, раскручивающуюся из начала координат (см. рис. П5).
Раскручивание спирали приводит к тому, что с течением времени увеличивается переменная Y 1, которую мы использовали для обозначения угловой величины φ из уравнения (35). Если величина φ вырастает настолько, что выполняется φ 2> ε , то знак перед производной первого порядка в уравнении (35) становится положительным. Тогда в первом из уравнений (38) мы получим, что B = — ε (при Y 1cm= 0), т. е. B < 0. Учитывая, что ∆ > 0; D < 0, и сравнивая с выражением (П25), приходим к заключению о том, что в этом случае стационарное решение (37) является устойчивым фокусом. Фазовая траектория представляет собой спираль, сходящуюся к началу координат (см. рис. П2).
Эволюционная диаграмма переменной Y 1показана на рис. 4. Штриховой линией обозначены фазовые траектории в пространстве Y 1, Y 2. Огибающие этих траекторий выделены. Вид сечения эволюционной диаграммы в месте сшивки двух конусов в координатах Y 1и Y 2совпадает с предельным циклом. При этом очевидно, что радиус спирали с течением времени стремится к значению √ ε по оси Y 1. Причем если речь идет о малом значении ε , т. е. о малой вязкости γ 0, то вид устойчивого стационарного решения закона (35) должен быть близок к уравнению окружности [2]:
Y 2 1ст+ Y 2 2ст≈ ε .
2.3.4.Таким образом, в фазовом пространстве двух переменных генератору Ван дер Поля соответствует устойчивая замкнутая траектория (аттрактор) – предельный цикл.
Сравнивая между собой эволюционные диаграммы, представленные на рис. 2 и 4, приходим к выводу об общих закономерностях возникновения устойчивых состояний описанных экономической и физической систем.
Читать дальше

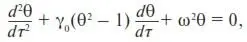 (34)
(34)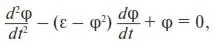 (35)
(35)