Пусть за время dt приобретается dy товара ( y – количество некоторого товара). Наблюдение за применением рекламы показывает, что в результате действия рекламы происходит ускорение приобретения товара с течением времени. Математически ускорение представляет собой вторую производную по времени, поэтому предыдущее утверждение можно записать в виде следующей пропорции:
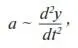
или
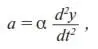 (3)
(3)
где a – потенциальное действие рекламы; α – коэффициент пропорциональности.
Уравнение (3) характеризует потенциальное действие рекламы. Однако на практике ее действие испытывает влияние различных факторов, как способствующих, так и мешающих восприятию рекламного материала. Все эти факторы разделяются на две основные группы: F 1– факторы, связанные с особенностями товара; и F 2– факторы, связанные с особенностями покупателя. Математически влияние этих групп можно учесть, добавив их в левую часть уравнения (3) (в левую, так как они влияют именно на действие рекламы a ):
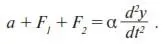 (4)
(4)
Перечень конкретных факторов, в той или иной степени имеющих отношение к группам F 1и F 2, может быть очень велик. Из этого перечня, следуя идее метода основных пропорций, мы выберем главные факторы, обязательно присутствующие в любой операции купли-продажи.
В группе F 1среди качеств товара, влияющих на восприятие рекламы, определяющим является уровень его доступности для покупателя. Действительно, какими бы достоинствами ни обладал товар и как бы необходим он ни был, его широкая доступность снижает актуальность любой информации о нем. Поэтому для группы F 1в качестве определяющего фактора мы выбираем насыщенность рынка данным товаром. Соответствующая пропорция имеет вид:
F 1~ y , откуда: F 1= – γy .
Здесь: γ – коэффициент пропорциональности, а минус указывает на то, что с увеличением количества товара на рынке снижается восприятие его рекламы (т. е. на то, что этот фактор должен уменьшать а в левой части уравнения (4)).
В группе F 2определяющим фактором является доход среднего покупателя. Это следует из того, что, каким бы желаемым ни был товар, если доход не позволяет его приобрести хотя бы в ближайшем будущем, то реакция на его рекламу будет снижена. На практике доход находит свое выражение через объем спроса. Последний же, как известно, представляет собой количество товара, который мог бы приобрести покупатель за определенный промежуток времени, что в математике соответствует первой производной по времени: dy/dt. Поэтому для этой группы факторов основная пропорция будет иметь вид:
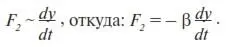
Здесь: β – коэффициент пропорциональности; минус указывает на разные знаки у dt (t ↑, dt > 0) и dy (y ↓ , dy < 0). Последнее следует из того, что в странах, в которых имеется инфляция, доход среднего покупателя с течением времени падает.
С учетом сказанного уравнение (4) запишется следующим образом:
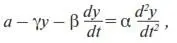
откуда
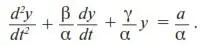 (5)
(5)
Это известное линейное неоднородное дифференциальное уравнение с постоянными коэффициентами (НОЛУ). Уравнение (5) решаем стандартными математическими методами (метод решения НОЛУ см. в Приложении, раздел П1.4):
y = y* + y 1, (6)
где y* – общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами (ОЛУ); y 1– частное решение НОЛУ.
Общее решение y* найдем из уравнения, в которое превращается (5) при замене правой части на 0. В этом случае НОЛУ переходит в ОЛУ (см. Приложение, раздел П1.3):
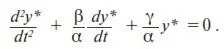 (7)
(7)
Воспользовавшись методикой решения ОЛУ, описанной в разделе П1.3 Приложения, составим и решим характеристическое уравнение:
Читать дальше

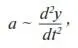
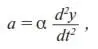 (3)
(3)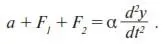 (4)
(4)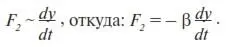
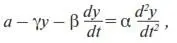
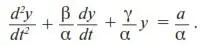 (5)
(5)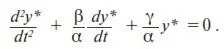 (7)
(7)









