Итак, в данной книге под переменными Y i в (1) мы понимаем макроскопические переменные, соответствующие некоторым обобщенным характеристикам коллективного движения элементов системы. Напомним, что в синергетике такие переменные называются параметрами порядка [19].
Математически создание синергетической модели, как правило, начинается с выбора параметров порядка, т. е. с выбора макроскопических переменных, количественно характеризующих основные связи в системе. Следующий шаг заключается в составлении пропорций, формирующих эти связи. Правило составления пропорций подробно описано в [19] (см. также [3]). Согласно этому правилу, увеличение некоторой величины с течением времени пропорционально приросту этой величины минус ее потери . Затем эти пропорции преобразуются в эволюционное уравнение типа (1).
Глава 1
Применение некоторых известных дифференциальных уравнений для создания моделей социальных и экономических систем
1.1. Экстремальное поведение большой группы людей
Если какой-либо объект представляет собой систему, то он обязательно подчиняется универсальным системным закономерностям. Социальные системы не являются исключением. В частности, коллективное поведение людей в простейшей экстремальной ситуации наглядно демонстрирует качества, которые могут наблюдаться в поведении, например, физических систем.
Допустим, что в здании находится большая группа людей. В некоторый момент времени, принятый за начальный, все люди пытаются выйти из здания. Мы хотим получить закон, показывающий, как с течением времени уменьшается число людей в здании [28].
Введем обозначения: N – количество людей, находящихся в здании в произвольный момент времени t; dN – количество людей, вышедших из здания за время dt . Сформулируем начальное условие: в момент времени t = 0 количество людей в здании равнялось N 0.
Составляем главную пропорцию задачи (см. введение, последний абзац). Делается это следующим образом. Из общих соображений можно предположить, что число людей, вышедших из здания за некоторый промежуток времени, пропорционально самому промежутку времени и количеству людей, находящихся в здании:
dN ~ dt, N .
Заменяя знак пропорции на коэффициент пропорциональности А , получим
dN = —ANdt,
или
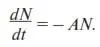
Эволюционное уравнение данной задачи (сравните с (1)). Появление минуса объясняется тем, что с увеличением t уменьшается N ( dN < 0).
Данное уравнение представляет собой известное дифференциальное уравнение с разделяющимися переменными. Поступаем согласно методу решения, описанному в разделе П1.2 Приложения. Сначала разделяем переменные по разные стороны уравнения, затем полученное выражение интегрируем:
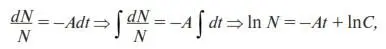
где C – постоянная интегрирования. Выразим N:
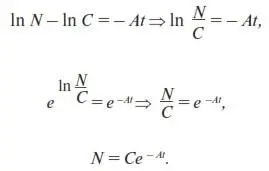 (2)
(2)
Постоянную C определим из начального условия. В нашей модели начальное условие будет выглядеть следующим образом (см. в Приложении формулу (П.1)):
N│ t = 0= N 0.
В соответствии с этим условием мы в (2) подставим t = 0 и N 0вместо N:
N 0= Ce – A ∙ 0= Ce 0= C.
Следовательно, C = N 0. Тогда (2) примет окончательный вид
N = N 0e —At.
Итак, мы получили закон, показывающий, как с течением времени уменьшается количество людей в здании. Здесь постоянная А характеризует архитектурные особенности здания: количество этажей, количество выходов и т. п.
Как видим, поведение людей, покидающих в экстремальной ситуации здание, будет таким, чтобы совместными действиями реализовать закон экспоненциального уменьшения числа людей в здании.
Нетрудно заметить, что данный закон по своему математическому виду совпадает с известным в физике законом радиоактивного распада:
N = N 0e —At; N – число нераспавшихся атомов,
что наглядно демонстрирует универсальность системного подхода к явлениям в природе и обществе.
1.2. Модель воздействия рекламы на количество покупаемого товара
(Изложение данного раздела следует работам [23, 28].) Как и в предыдущем разделе, мы воспользуемся методом составления главных пропорций.
Читать дальше

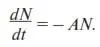
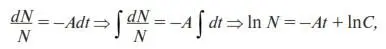
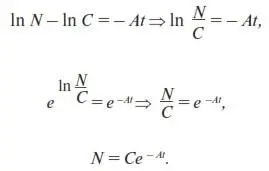 (2)
(2)









