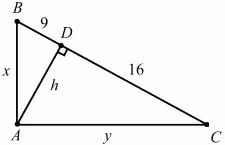
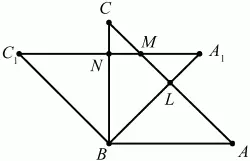
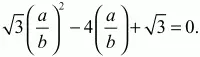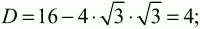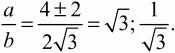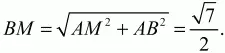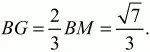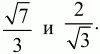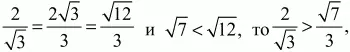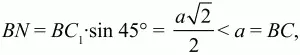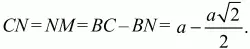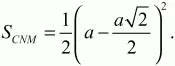Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс
Здесь есть возможность читать онлайн «Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: Математика4, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Геометрия: Планиметрия в тезисах и решениях. 9 класс
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Геометрия: Планиметрия в тезисах и решениях. 9 класс: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Геометрия: Планиметрия в тезисах и решениях. 9 класс»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Материалы пособия соответствуют учебной программе школьного курса геометрии.
Для учителей и учащихся 9-х классов.