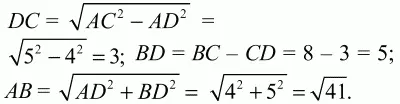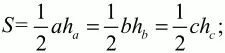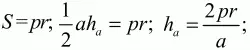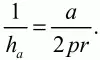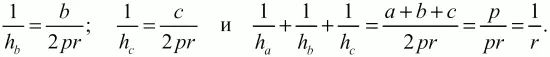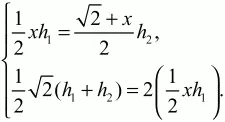Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

1. Формула расстояния от точки А(х0, у0) до прямой ах + by + с = 0.

2. Значения sin, cos, tg, ctg от углов 30°, 45° и 60°.

3. Докажите, что если треугольники подобны, то с тем же коэффициентом пропорциональны произвольные соответствующие линейные элементы этих треугольников.

4. В треугольнике ABC длина стороны АС равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что площадь треугольника ABC меньше 3.

5. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка О так, что OB = OD = 13. Найти расстояние от точки О до наиболее удалённой от нее вершины прямоугольника.

1. Координаты на плоскости. Расстояние между точками.

2. Теорема косинусов. Связь теоремы косинусов и теоремы Пифагора.

3. Площадь четырёхугольника, правильного n-угольника.

4. В треугольнике ABC медианы, проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ.

5. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки.

1. Уравнение фигуры. Уравнение окружности.

2. Базис на плоскости. Теорема о разложении вектора по базису.

3. Формула S = рr для треугольника.

4. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади.

5. На сторонах АВ и АС треугольника ABC взяты точки М и Т, такие, что AM/MB = CN/NA = 1/2. Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.

1. Касательная к окружности, её свойство. Виды касания окружностей.

2. Координатные формулы движений.

3. Формула S = abc/4R для треугольника.

4. В треугольнике ABC угол А прямой, величина угла В равна 30°. В треугольник вписана окружность, радиус которой равен ?3. Найти расстояние от вершины С до точки касания этой окружности с катетом АВ.

5. Основания трапеции равны 4 см и 9 см, а диагонали равны 5 см и 12 см. Найти площадь трапеции и угол между её диагоналями.

1. Пропорциональность отрезков хорд и секущих окружности.

2. Первая теорема косинусов для четырёхугольника.

3. Свойство средней линии треугольника и трапеции.

4. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника.

5. Средняя линия трапеции равна 4, отрезок, соединяющий середины оснований, равен 1, углы при основании трапеции равны 40° и 50°. Найдите длины оснований трапеции.

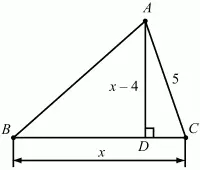
Рис. 220.

Решение. Пусть ВС = х, тогда AD = х – 4. Площадь треугольника ABC равна 1/2 ? ВС ? AD = 1/2 ? х ? (х – 4). По условию площадь равна 16. Значит, 1/2 ? х ? (х – 4) = 16, откуда х = 8. BС = 8, AD = BС – 4 = 4. По теореме Пифагора

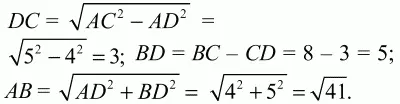
Периметр треугольника равен PABC = AC + BC + AB = 5 + 8 + ?41 = 13 + ?41.

Ответ: 13 + ?41 см.

Решение. Запишем площадь треугольника тремя способами:

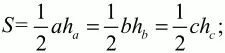
c другой стороны,

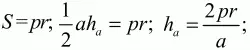
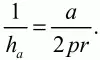
Аналогично

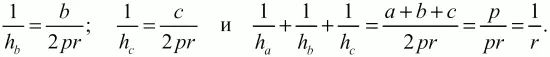
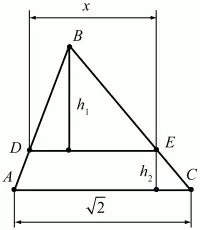
Рис. 221.

Решение. Пусть в треугольнике ABC АС = ?2. Проведем отрезок DE так, что площадь треугольника DBE равна площади трапеции ADEC. Так как нам нужно найти длину отрезка DE, обозначим ее через х. Введем еще обозначения: высоту треугольника DBE обозначим через h1 высоту трапеции ADEC через h2 Составим систему уравнений:

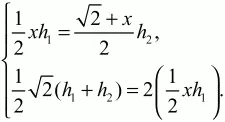
Первое уравнение фиксирует равенство площадей треугольника DBE и трапеции ADEC. Второе уравнение констатирует тот факт, что площадь треугольника ABC в 2 раза больше площади треугольника DBE, при этом использовано условие АС = ?2. Решая систему, получаем: