Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

2. Формулы приведения.

3. Теорема Менелая и обратная к ней.

4. Центр О окружности радиуса 3 лежит на гипотенузе АС прямоугольного треугольника ABC. Катеты треугольника касаются окружности. Найти площадь треугольника ABC, если известно, что длина отрезка ОС равна 5.

5. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки M и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция.

1. Геометрическое место центров вписанной в треугольник и описанной около треугольника окружностей.

2. Теорема Чевы и обратная к ней.

3. Многоугольники. Правильные многоугольники. Формулы R и r для правильного n-угольника со стороной а.

4. На плоскости лежит равнобедренный прямоугольный треугольник, у которого катеты имеют длину а. Поворотом в этой плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается другой равнобедренный прямоугольный треугольник. Найти площадь четырёхугольника, являющегося общей частью этих двух треугольников.

5. В параллелограмме ABCD сторона АВ равна 6 см, а высота, проведенная к основанию AD, равна 3 см. Биссектриса угла BAD пересекает сторону ВС в точке М так, что МС = 4 см. N – точка пересечения биссектрисы AM и диагонали BD. Вычислить площадь треугольника BNM.

1. Векторное произведение векторов, его геометрический смысл.

2. Использование теорем синусов и косинусов для решения треугольников.

3. Свойства ромба, прямоугольника, квадрата.

4. На плоскости даны две окружности радиусов 12 см и 7 см с центрами в точках О1 и O2, касающиеся некоторой прямой в точках М1 и М2 и лежащие по одну сторону от этой прямой. Отношение длины отрезка M1M2 к длине отрезка О1O2 равно

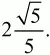
Вычислить длину отрезка М1М2.

5. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка М – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны.

1. Признаки и свойства параллелограмма.

2. Формула Эйлера о расстоянии между центрами вписанной в треугольник и описанной около треугольника окружностей.

3. Геометрическое введение синуса, косинуса, тангенса, котангенса. Основные тригонометрические тождества.

4. В треугольниках ABC и А1В1С1 длина стороны АВ равна длине стороны А1В1, длина стороны АС равна длине стороны А1С1, величина угла ВАС равна 60° и величина угла В1А1С1 равна 120°. Известно, что отношение длины В1С1 к длине ВС равно ?n (где n – целое число). Найти отношение длины АВ к длине АС. При каких значениях n задача имеет хотя бы одно решение?

5. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4.

1. Аксиоматический подход в геометрии. Требования к системе аксиом. Аксиоматическая теория.

2. Теорема синусов. Формула 2R = a/sin ?.

3. Вписанные в окружность углы. Соотношение между вписанным и центральным углами, опирающимися на одну дугу.

4. В трапеции ABCD отрезки АВ и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найти площадь треугольника ВСЕ, если АВ = 30 см, DC = 24 см, AD = 3 см и ?DAB = ?/3.

5. В прямоугольный треугольник, периметр которого равен 36 см, вписана окружность. Гипотенуза делится точкой касания в отношении 2:3. Найти длины сторон треугольника.

1. Теорема Фалеса. Теорема о пропорциональных отрезках.

2. Длина медианы треугольника.

3. Скалярное произведение векторов. Угол между векторами. Угол между прямыми.

4. Хорды АВ и АС имеют одинаковую длину. Величина образованного ими вписанного в окружность угла равна ?/6. Найти отношение площади той части круга, которая заключена в этом угле, к площади всего круга.

5. Внутри равностороннего треугольника ABC дана точка М, такая, что AM = 1, ВМ = ?3 и СМ = 2. Найти АВ, ?АМВ и ?ВМС.

1. Теорема Пифагора. Египетский треугольник.

2. Длина биссектрисы треугольника.

3. Понятие площади фигуры. Площадь прямоугольника, параллелограмма, треугольника, трапеции.

4. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство: РА2+ РВ2+ PC2? 1/3(АВ2+ ВС2+ СА2).

5. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата.