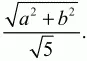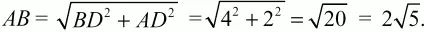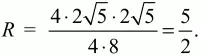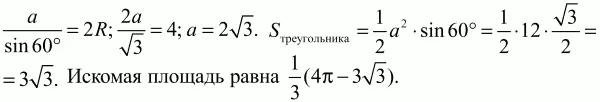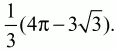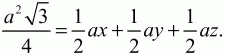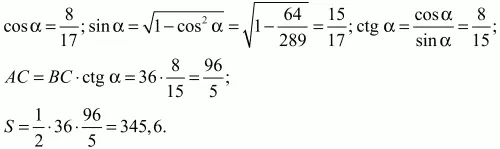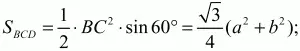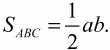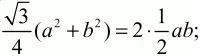Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

Ответ:

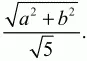
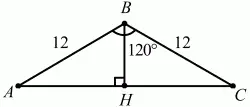
Рис. 227.

Решение. Пусть в треугольнике ABC АВ = ВС = 12, ?ABC = 120°. Так как в треугольнике сумма углов равна 180°, то ?А + ?С = 180° – 120° = 60°. Учитывая, что в равнобедренном треугольнике углы при основании равны, получаем: ?А = 30°. Рассмотрим треугольник ВНА, где ВН – высота треугольника. ВН – катет в этом треугольнике, лежащий напротив угла в 30°.

Тогда ВН = 1/2 ? АВ = 6.

Ответ: 6.

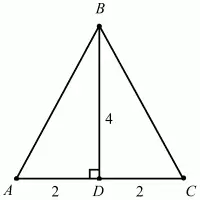
Рис. 228.

Решение. Поскольку высота в равнобедренном треугольнике, проведённая к основанию, является и медианой треугольника, то AD = DC = 2. Тогда по теореме Пифагора имеем:

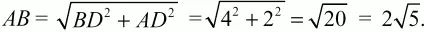
Естественно, что и ВС = 2?5. Воспользуемся формулой радиуса описанной около треугольника окружности R = abc/4S. Длины сторон треугольника равны 4, 2?5, 2?5, а площадь треугольника S = 1/2 ? AC ? BD = 1/2 ? 4 ? 4 = 8;

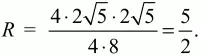
Тогда площадь круга Sкруга = ?R2= 25?/4.

Ответ: 25?/4.

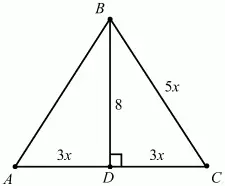
Рис. 229.

Решение. Так как BD – высота в равнобедренном треугольнике ABC, то она является и медианой, т. е. AD = DC. Так как AC/BC = 6/5, то можно обозначить DC = Зх; ВС = 5х (см. рис.). Из ?BCD по теореме Пифагора DB2+ DC2= ВС2. Или 82+ (Зх)2= (5х)2; х = 2. Радиус вписанной окружности r = S/P; площадь треугольника S = 1/2 АС ? BD = 1/2 ? 6х ? 8 = 48; полупериметр р = (5x + 5x + 6x)/2 = 16; r = 48/16 =3.

Ответ: 3.

Решение. Sзаштрихованного сектора = 1/3(Sкруга – Sтреугольника). Длина окружности l = 2?R. По условию l = 4?; 2?R = 4?; R = 2. Sкpyгa = ?R2= 4?. Длину стороны треугольника найдём по теореме синусов:

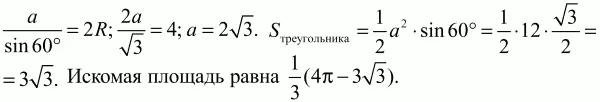
Ответ:

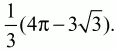
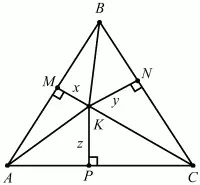
Рис. 230.

Решение. Пусть К – произвольная точка внутри равностороннего треугольника ABC со стороной а. Опустим перпендикуляры KM, KN, КР на стороны треугольника. Обозначим эти перпендикуляры следующим образом: КМ = х, KN = у, КР = z. Тогда SABC = SABK + SBKC + SAKC. Получаем равенство:

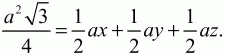
Отсюда (a?3)/2 = x + y + z. Но высота h треугольника равна h = a ? sin 60° = (a?3)/2; значит, х + у + z = h.

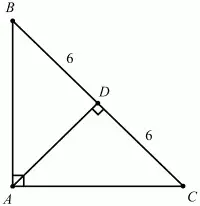
Рис. 231.

Решение. Так как AD – высота в равнобедренном треугольнике ABC, то она является и медианой. Значит, BD = DC = 6. Тогда AD = BD = 6, так как ?ABD = ?BAD = 45°.

Можно было увидеть и другую закономерность. Так как D – середина гипотенузы, то D – центр описанной около треугольника ABC окружности. Значит. DA = DB = DC = 6.

Ответ: 6 см.

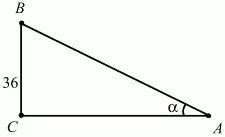
Рис. 232.

Решение. Обозначим угол ВАС через ?. Тогда AC = BC ? ctg?. Последовательно находим:

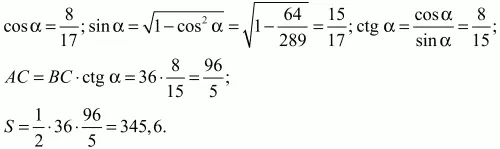
Ответ: 96/5; 345, 6

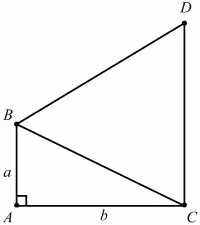
Рис. 233.

Решение. Обозначим катеты прямоугольного треугольника ABC с гипотенузой ВС через а и b (см. рис). Тогда

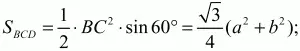
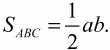
По условию SBCD = 2SABC. Значит,

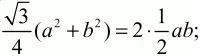
преобразуем это уравнение к виду