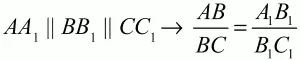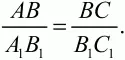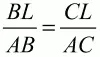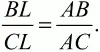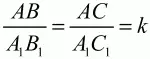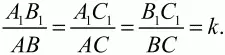Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки (рис. 83).
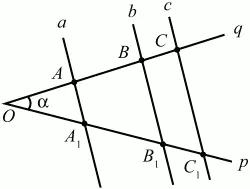
Рис. 83.
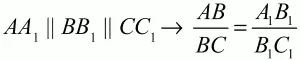
или
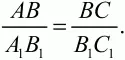
Свойство биссектрисы треугольника.
Биссектриса угла треугольника делит противолежащую ему сторону на отрезки, пропорциональные двум другим сторонам (рис. 84).
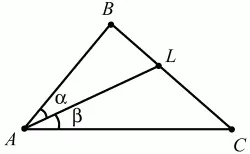
Рис. 84.
Если ? = ?, то
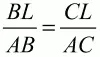
или
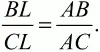
Признаки подобия треугольников.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны (рис. 85).
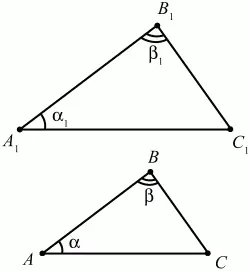
Рис. 85.
Треугольники ABC и A1B1C1 – подобные, т. к. ? = ?1 и ? = ?1.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то треугольники подобны (рис. 86).
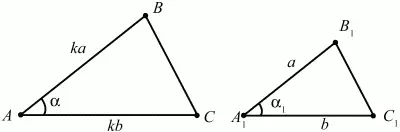
Рис. 86.
Треугольники ABC и A1B1C1 – подобны, т. к.
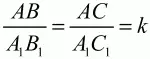
и ? = ?1.
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны (рис. 87).
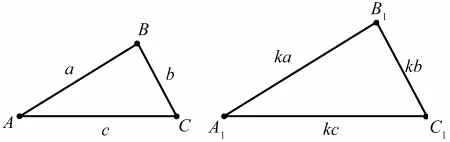
Рис. 87.
Треугольники ABC и A1B1C1 – подобны, т. к
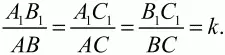
5. Основные геометрические неравенства
Соотношение длин наклонной и перпендикуляра.
Если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше (рис. 88):
АА' < АВ < АС; если А'С > А'В, то АС > АВ.
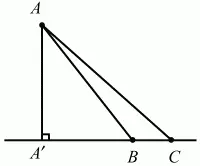
Рис. 88.
Неравенство треугольника.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон (рис. 89):
АС < АВ + ВС.
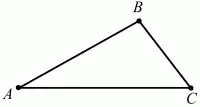
Рис. 89.
Связь между величинами сторон и величинами углов в треугольнике.
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол (рис. 90).
(BC < AB < AC) ? (?А < ?С < ?В).
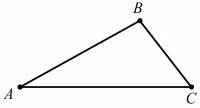
Рис. 90.
6. Основные геометрические места точек на плоскости
Геометрическим местом точек плоскости, равноудалённых от сторон угла, будет биссектриса данного угла (рис. 91).
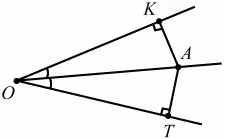
Рис. 91.
АК = AT, где А – любая точка на биссектрисе.
Геометрическим местом точек, равноудалённых от двух данных точек, будет прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину (рис. 92).
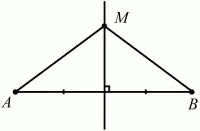
Рис. 92.
MA = MB, где М – произвольная точка на серединном перпендикуляре отрезка АВ.
Геометрическим местом точек плоскости, равноудалённых от заданной точки, будет окружность с центром в этой точке (рис. 93).
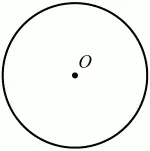
Рис. 93.
Точка О равноудалена от точек окружности.
Местоположение центра окружности, описанной около треугольника.
Читать дальше
Конец ознакомительного отрывка
Купить книгу