Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

49. В чём состоит сущность метода геометрических мест, используемого при решении задач на построение? (2)

50. Что такое ломаная? (1)

51. Какая ломаная называется замкнутой? (1)

52. Дайте определение многоугольника (на плоскости). Нарисуйте произвольный пятиугольник, отметьте его вершины и проведите в нём все диагонали. (1)

53. Какой многоугольник называется выпуклым? (1)

54. Какой многоугольник называется правильным? (1)

55. Какой многоугольник называется: вписанным в окружность; описанным около окружности? (1)

56. Что называют периметром многоугольника? (1)

57. Дайте определение параллелограмма. (1)

58. Дайте определение прямоугольника. (1)

59. Дайте определение ромба. (1)

60. Дайте различные определения квадрата. (1)

61. Дайте определение трапеции. Какие стороны трапеции называются основаниями, какие – боковыми сторонами? (1)

62. Какая трапеция называется равнобокой? (1)

63. Что называют средней линией трапеции? (1)

64. Что называют наклонной, проведённой из точки, не лежащей на прямой, на эту прямую? Что называют проекцией этой наклонной? (1)

65. Как на плоскости вводится декартова система координат? (1)

66. Что такое абсцисса и ордината точки? (1)

67. Что называют уравнением фигуры? (1)

68. Какой геометрический смысл имеет число k в уравнении прямой у = kx + в?(1)

69. Что такое движение? (1)

70. Назовите виды движений на плоскости. Покажите на конкретных примерах, как построить образы фигур при данных видах движений. (1)

71. Какие два луча называются сонаправленными и противоположно направленными? (1)

72. Что такое вектор? Как обозначать вектор? (1)

73. Какие два вектора называются одинаково направленными и противоположно направленными? (1)

74. Что такое абсолютная величина (модуль) вектора? (1)

75. Какой вектор называют нулевым? (1)

76. Какие два вектора назьшают равными? (1)

77. Как вводятся координаты вектора через координаты его начала и конца? (1)

78. Что называют суммой векторов? Нарисуйте два произвольных вектора и покажите их сумму. (1)

79. Что назьшают разностью векторов? Нарисуйте два произвольных вектора и покажите их разность. (1)

80. Что называют проекцией вектора на ось? Покажите на рисунке. (1)

81. Что называют произведением вектора на число? Нарисуйте произвольный вектор а, а также b = 2а и с = -1/2а (1)

82. Что значит разложить вектор а по векторам b и с? (1)

83. Дайте определение скалярного произведения векторов. (1)

84. Что называют углом между векторами? Чем отличается угол между векторами от угла между прямыми? (1)

85. В каком случае скалярное произведение векторов равно нулю? (1)

86. Дайте определение координатного вектора (орта). (1)

87. Какое преобразование называется преобразованием подобия? (1)

88. Что такое гомотетия? (1)

89. Какие фигуры называются подобными? Как обозначать подобие фигур? (1)

90. Что называют центральным углом в окружности? (1)

91. Как определить градусную меру дуги окружности? (1)

92. Какой угол называется вписанным в окружность? (1)

93. Как в курсе геометрии вводится понятие площади? (2)

1. Замечательные точки в треугольнике. (1)

2. Вневписанные окружности. (1–2)

3. Радикальная ось и радикальный центр окружностей. Пучки окружностей. (3)

4. Полярное соответствие. Принцип двойственности в геометрии. (3)

5. Отображения и преобразования множеств. Композиция преобразований. Аффинные преобразования плоскости. (3)

6. Инверсия плоскости относительно окружности. (3)

7. Понятие длины. Расстояние между фигурами. (2)

Приведём без доказательства основные теоремы планиметрии.

Доказательства желательно изучать по вашему учебнику. Опасно изучать доказательство теорем по разным учебным пособиям – можно в погоне за простотой попасться на капкане «порочного круга». Приведём простой пример. Нужно доказать признаки параллельных прямых (если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны).

На рис. 56:m, n, a – прямые. Точка А – точка пересечения прямых m и а, В – точка пересечения прямых n и а.

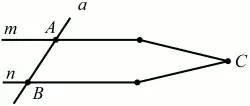
Рис. 56.

Ученик привёл простое доказательство: если бы прямые m и n пересекались в некоторой точке С, то тогда из того, что сумма углов в треугольнике АСВ равна 180°, следует, что ?АСВ = 0°, что невозможно. Значит, прямые m и n параллельны.