Андрей Павлов - Геометрия - Планиметрия в тезисах и решениях. 9 класс

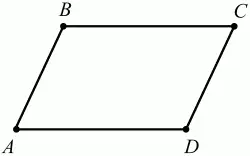
Рис. 41.

ABCD – параллелограмм, т. к. ВС||AD и АВ||CD.

Прямоугольник – это параллелограмм, у которого все углы прямые (рис. 42).

Рис. 42.

ABCD – прямоугольник, т. к. ?А = ?В = ?С = ?D = 90°.

Ромб – это параллелограмм, у которого все стороны равны (рис. 43).

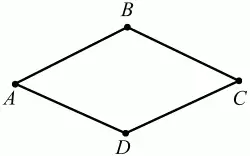
Рис. 43.

ABCD – ромб, т. к. AD||ВС и АВ||DC и AB = BC = CD = AD.

Квадрат – это прямоугольник, у которого все стороны равны. Можно также сказать, что квадрат – это ромб, у которого все углы прямые (рис. 44).

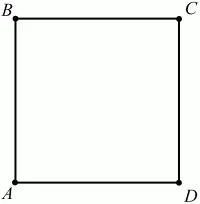
Рис. 44.

ABCD – квадрат, т. к. ?А = ?В = ?С = ?D = 90° и АВ = ВС = CD = DA.

Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами (рис. 45).

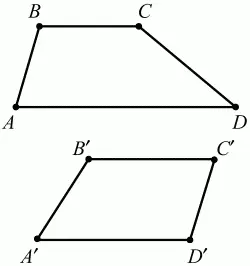
Рис. 45.

ABCD и А' В' С' D' – трапеции, т. к. BC||AD, BC||AD.

Трапеция, у которой боковые стороны равны, называется раенобокой (рис. 46).

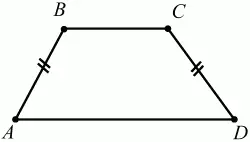
Рис. 46.

ABCD – равнобедренная трапеция (АВ = CD).

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции (рис. 47).

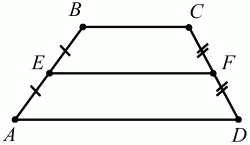
Рис. 47.

EF – средняя линия трапеции ABCD: AE = EB, DF = FC.

Пусть ВА – перпендикуляр, опущенный из точки В на прямую а, и С – любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а. Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной (рис. 48).

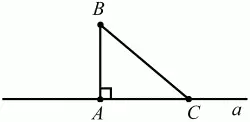
Рис. 48.

ВА – перпендикуляр к прямой а, ВС – наклонная.

Проведём на плоскости через точку О две взаимно перпендикулярные прямые х и у – оси координат. Ось х (она обычно горизонтальная) называется осью абсцисс, а ось у – осью ординат. Точкой пересечения О – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из полуосей каждой оси называть положительной, отмечая её стрелкой, а другую – отрицательной.

Каждой точке А плоскости мы сопоставим пару чисел – координаты точки – абсциссу х и ординату у по следующему правилу.

Через точку А проведём прямую, параллельную оси ординат. Она пересечёт ось абсцисс х в некоторой точке Аx. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Аx. Это число будет положительным, если Аx принадлежит положительной полуоси и отрицательным, если А принадлежит отрицательной полуоси. Если точка А лежит на оси ординат y, то полагаем х равным нулю.

Ордината j точки А определяется аналогично. Через точку А проведём прямую, параллельную оси абсцисс х. Она пересечёт ось ординату в некоторой точке Аy. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки Аy. Это число будет положительным, если Аy принадлежит положительной полуоси, и отрицательным, если А принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс х, то полагаем у равным нулю.

Координаты точки записывают в скобках рядом с буквенным обозначением точки, например: А(х; у) (на первом месте абсцисса, на втором – ордината) (рис. 49).

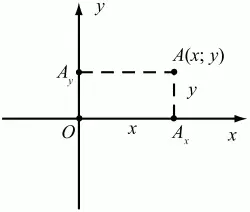
Рис. 49.

Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры.

Например, уравнение прямой у = kx + b, где k – тангенс угла наклона прямой к оси Ох (рис. 50).

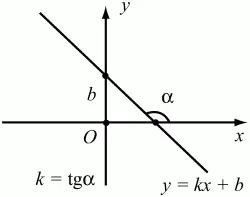
Рис. 50.

Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной. Симметрия относительно точки, симметрия относительно прямой, поворот, параллельный перенос – виды движений.