Josep Carrera - Трехмерный мир. Евклид. Геометрия

Доказательство Евклида из предложения 47 книги I.

Теорема Пифагора.В прямоугольном треугольнике ΔАВС квадрат на гипотенузе ВС равен сумме квадратов, построенных на катетах АВ и АС.

Как видно на рисунке 8, из вершины А проводится прямая, перпендикулярная гипотенузе ВС, до пересечения со стороной Н1 квадрата В1. Мы получаем прямоугольники CJ и В]. Необходимо доказать, что прямоугольник С] равен квадрату AD и что прямоугольник BJ равен квадрату AG. Евклид строит треугольники AACI и ADCB. Они равны, как можно легко убедиться, поскольку имеют равные стороны и угол между ними (общее понятие 2). Итак, у треугольника AACI и прямоугольника CJ общая сторона СI, а его вершина А находится на той же параллельной прямой, AJ, на которой у прямоугольника CJ расположена сторона KJ, противоположная стороне CI. Следовательно, площадь прямоугольника CJ в два раза больше площади треугольника ΔACI. Таким же образом, площадь квадрата AD в два раза больше площади треугольника ADCB. Следовательно, площадь квадрата AD равна площади прямоугольника IK (первое равенство, которое мы должны были доказать). Аналогично, площадь квадрата AG равна площади прямоугольника BJ (второе равенство, которое мы хотели доказать). Следовательно, согласно общему понятию 2, теорема доказана.

Термин «геометрическая алгебра» в свое время вызывал споры, но в любом случае он очень удобен из-за своей лаконичности. Дисциплина заключается в том, чтобы выразить площади прямоугольников и квадратов в числовой форме. Ее пионерами были Диофант Александрийский и арабские математики. Например, знаменитое дистрибутивное свойство умножения, представленное в алгебраическом виде как а (b + с + d +...) = (a x b) + (a x c) + + (а х d) + ..., в геометрии Евклида будет записано так:

Книга II,предложение 1.

Если имеются две прямые и одна из них рассечена на сколько угодно отрезков, то прямоугольнику заключающийся между этими двумя прямыми у равен вместе взятым прямоугольникам, заключенным между нерассеченной прямой и каждым из отрезков (см. рисунок 9).

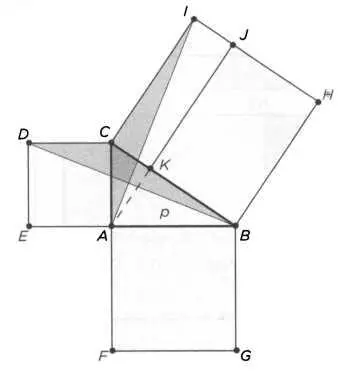
РИС. 8

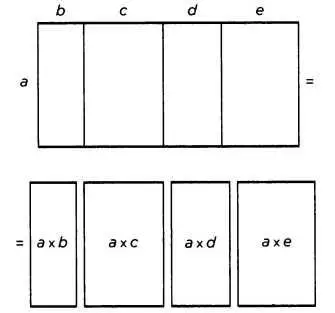
РИС. 9

Аналогичным образом можно выразить и другие алгебраические равенства, например (а ± b) ²= а ²+ b ²± 2ab y(а + b) х (а - b) = а ²- b ². Рассмотрим только (а + b) х (а - b) = а ²- b ². Будем исходить из альтернативной формулировки предложения 5 книги 2. Возьмем фигуру, как на рисунке 10. Разобьем прямоугольник HJ. В первую очередь установим равновеликость прямоугольников FN и NB, используя свойства гномона. Прямоугольник NB равновелик прямоугольнику BI по построению, так как DB = DF = а, BJ = FH = b, DJ = а + b, JI = DH = а - b. Получается, что прямоугольник HJ состоит из квадрата KD (а ²), поскольку прямоугольники GJ и FN равны, но остается квадрат MG (b ²).

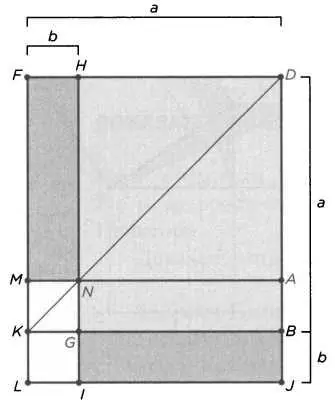
РИС. 10

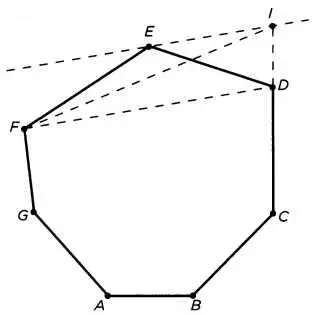
РИС. 11

Второе применение танграма позволяет доказать, что многосторонние фигуры могут трансформироваться в равновеликий квадрат. Для доказательства мы будем постепенно уменьшать количество сторон многосторонней фигуры, сведя ее к треугольнику. Возьмем многостороннюю фигуру ABCDEFG (см. рисунок 11). Соединим две ее любые вершины, между которыми есть хотя бы одна другая вершина, например D и F. Проведем параллельную прямую через вершину Е. Продлим сторону CD, пока она не пересечет эту параллельную в точке I. Соединим точки I и F. Треугольники IFD и EFD равновеликие (книга I, предложение 35). Таким образом, фигуры ABCDEFG и ABCIFG также равновеликие, но у первой на одну сторону больше, чем у второй. Повторив эту процедуру, мы получим прямоугольник, равновеликий заданному многоугольнику. Следовательно, всякую многоугольную фигуру можно свести к треугольнику.

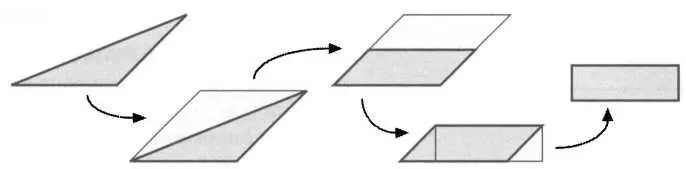
РИС. 12

Затем мы можем доказать, что любой треугольник можно преобразовать в прямоугольник, что наглядно показано на рисунке 12.

Остается разобрать последний вариант: доказать, что всякий прямоугольник можно свести к квадрату (книга II, предложение 14). Возьмем прямоугольник AD и попробуем преобразовать его в квадрат. Рассмотрим рисунок 13. Отложим отрезок, равный CD, на продолжении стороны АС. Разделим отрезок АВ пополам точкой G. Проведем полуокружность с центром G и радиусом GB и полухорду FC, перпендикулярную АВ и пересекающую ее в точке С. Отрезок FC будет стороной квадрата, равновеликого данному прямоугольнику.