Владимир Трошин - Натуральные числа. Этюды, вариации, упражнения

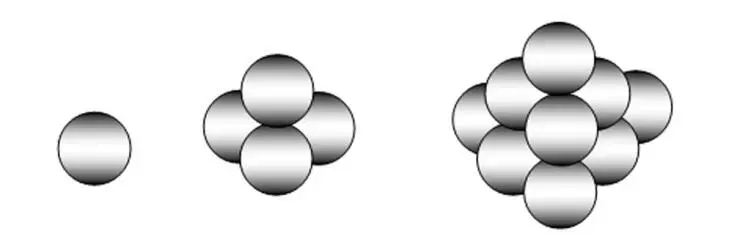
Затем к пирамидальным числам отнесем квадратные пирамидальные числа, представляющие собой количество сложенных сфер в пирамиде с квадратным основанием. И далее, далее … .

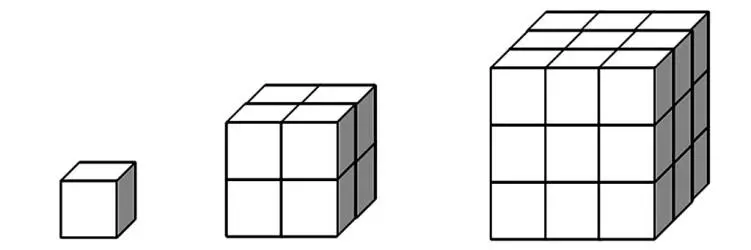
Кубические числа возникают при складывании кубиков: 1, 2·2·2=8, 3·3·3=27, 4·4·4=64, 5·5·5=125… , то есть это просто кубы натуральных чисел.

В любом рассмотренном варианте фигурных чисел возможны продолжения. Некоторые из них мы отнесли во второй уровень классификации и все равно перебрать это многообразие невозможно. Причем, у каждого из этих видов чисел открыты свои свойства, о которых здесь не рассказано. Целью этой книги не является подробное описание свойств всех существующих групп натуральных чисел. Задача ставится иная: легкими штрихами наметить общую картину, заинтересовать читателя, который возможно сам продолжит рассмотрение понравившегося ему класса чисел, и тогда уж изучит все их свойства по другим источникам, а возможно сделает свои открытия. Вот где простор для тематики ученической проектной деятельности. Каждому ученику поручить исследование отдельного вида чисел, их хватит на целый класс.

Столкнувшись с тем многообразием, которое скрыто в одних только натуральных числах, понимаешь, для чего могла бы пригодиться бесконечная жизнь – изучать эти числа.

С другой стороны, поставьте себя на место древних пифагорейцев. Телевизоров нет, смартфонов нет, развлечений кот наплакал. Поэтому они и развлекались с натуральными числами и достигли в этом таких высот, которые современный человек вряд ли охватит своим умом. Причем учтите, во времена пифагорейцев занимались математикой и философией люди свободные от других забот, не ведающие иного труда, кроме умственного. Даже в умственной деятельности теоретические исследования считались достойными привилегированного класса, а чисто вычислительная, практическая деятельность поручалась низшим сословиям. В наше время нет привилегированных классов и большинству людей не до чисел, ведь жизнь с развитием цивилизации легче не становится. Но как в любой другой области, среди множества людей разумных есть и любители исследовать числа.

Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие математики античности (Эратосфен, Диофант), большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Кардано), выдающиеся умы более позднего времени (Ферма, Эйлер, Гаусс). Все результаты, которых они достигли не описать и в нескольких книгах. В частности Диофант знал формулу, связывающую треугольные и квадратные числа: 8 P n (3)= P n (4). Были выведены общие формулы представления n -го по порядку k -угольного числа. Ферма сформулировал в 1637 году так называемую «золотую теорему»: Всякое натуральное число – либо треугольное, либо сумма двух или трёх треугольных чисел.

Всякое натуральное число – либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел.

Всякое натуральное число – либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел; и т.д.

Полное доказательство этой теоремы сумел дать Коши в 1813 году. Оцените промежуток времени, потребовавшийся для доказательства одной теоремы: с 1637 до 1813 года.

Последние годы в занимательной математике много пишется о числах, имеющих специфическое представление в виде цифр. В первую очередь речь идет о числах – палиндромах . Это понятие пришло в математику из языка, где палиндром (от греч. pal i ndromos – бегущий обратно), слово, фраза или стих, которые могут читаться (по буквам или по словам) спереди назад и с конца вперед, давая одинаковый смысл. В русском языке палиндромами являются, например, такие слова: довод, доход, заказ, радар и другие. Некоторые палиндромы, если их написать печатными буквами, не только читаются одинаково слева направо и наоборот, но обладают осью симметрии, например, поп, потоп, топот. Палиндромы известны во многих языках (например, gig (кабриолет), eve (канун), level (уровень) – в английском), а их история восходит к временам незапамятным. Чтобы не нарушать принятый в книге принцип давать классам чисел название в виде прилагательного, назовем такие числа палинромическими числами.