Плоские числа – числа, составные, представимые в виде произведения двух сомножителей больших единицы: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, … .
Телесные числа – числа, представимые произведением трёх сомножителей больших единицы: 8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, … .
Эти определения приводятся в «Началах» Евклида. Мне не очень нравится, что при подобном подходе многие числа попадают одновременно в два различных вида. Например, 8=2·4=2·2·2, 12=2·6=3·4=2·2·3, 18=2·9=3·6=2·3·3 и так далее.
Критерии – геометрическая интерпретация
Многоугольные числа – числа, ассоциированные с определённым многоугольником, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры – треугольника, квадрата и так далее. Про точки может быть не совсем корректно говорить, так как в математике точка – это абстрактное понятие, не имеющее линейных размеров, поэтому будем подразумевать некие круглые фишки одинаковых размеров, из которых и выкладываются геометрические фигуры. Ряд фигур будем начинать с одной фишки, а затем достраиваем до равностороннего треугольника со стороной в две фишки, в три фишки и так далее.
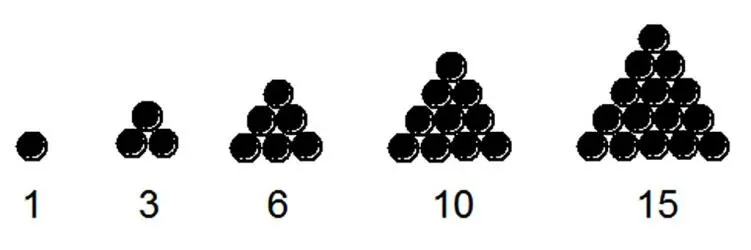
Получаем треугольные числа: 1, 3, 6, 10, 15, 21, 28, 36, 45, … . Треугольные числа можно получить и без геометрической интерпретации посредством последовательного суммирования чисел натурального ряда: 1, 1+2=3, 1+2+3=6, 1+2+3+4=10, 1+2+3+4+5=15, … . Формула для получения n -го треугольного числа: P n ( 3)=( n ( n +1))/2. Сумма двух последовательных треугольных чисел дает полный квадрат: P n ( 3) + P n + 1 (3)=( n +1) 2. Четность элементов последовательности меняется с периодом 4: нечетное, нечетное, четное, четное.
Извините, формулы получаются написанными коряво, так как конвертер издательства не принимает и не распознает формулы, красиво сделанные во встроенном редакторе формул, и приходится изощряться, чтобы написать их в Worde просто с клавиатуры. В результате остается только изображение в строчку, красота формулы теряется.
Получение квадратных чисел можно иллюстрировать построением квадратов с последовательным увеличением длины стороны квадрата: 1, 4, 9, 16, 25, 36, 49, … .
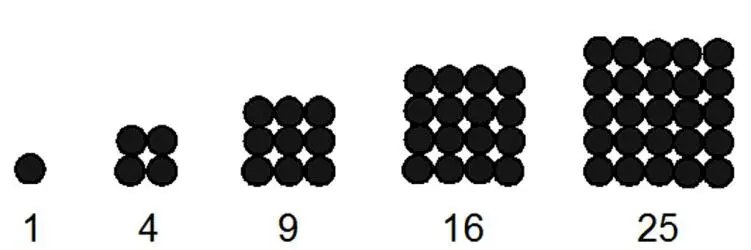
С алгебраической точки зрения они представляют собой квадраты чисел натурального ряда, но могут быть интерпретированы и как результат последовательного суммирования нечетных чисел натурального ряда: 1+3=4, 1+3+5=9, 1+3+5+7=16, 1+3+5+7+9=25. Формула для получения n -го квадратного числа P n (4)= n 2. Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел: 4=1+3, 9=3+6, 16=6+10, P n (4)= P n - 1 (3) + P n (3). До сих пор не доказана гипотеза Лежандра (1808 год): между последовательными квадратными числами всегда найдётся простое число. Не доказана, но и не опровергнута.
Частным случаем плоских чисел являются прямоугольные числа, являющиеся произведением двух последовательных натуральных чисел: 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, … .
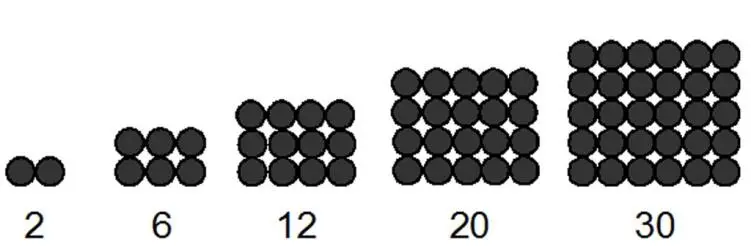
Прямоугольные числа представляют собой удвоенные треугольные числа: P n ( np )= n ( n -1).
Вернемся к правильным многоугольникам. На очереди пятиугольные числа: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, … .
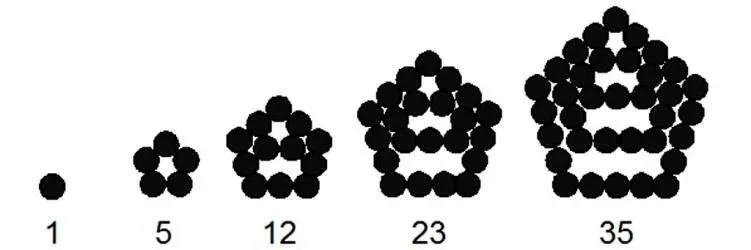
Формула для получения n -го пятиугольного числа: P n ( 5)=( n (3 n -1))/2.
Далее идут шестиугольные числа: 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, ….
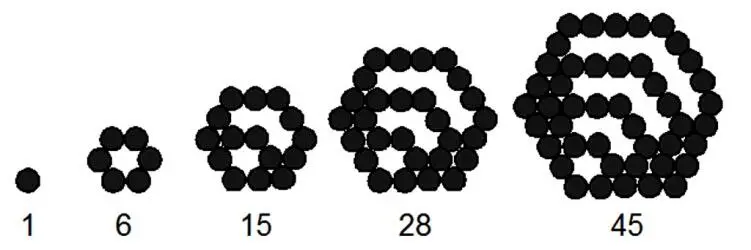
Формула для получения n -го шестиугольного числа: P n ( 6)=2 n 2- n . Последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами: P n ( 6)= P 2 n - 1 (3).
Можно было бы продолжать бесконечно, рассматривая прочие многоугольные плоские фигурные числа, но нужно где-то остановиться. Пусть это будут шестиугольные числа.
Выйдя из плоскости можно рассмотреть трехмерные правильные фигурные числа. Пирамидальные числа возникают при складывании маленьких шаров одинакового диаметра горкой так, чтобы они не раскатывались. Получается пирамида. Первые из них тетраэдрические числа – это фигурные числа, которые представляют собой пирамиду, сложенную из сфер одного диаметра. Каждый слой в такой пирамиде – треугольное число. Наверху один шар, под ним – 3, под теми – 6 и т. д.: 1, 1+3=4, 1+3+6=10, 1+3+6+10=20, … . Пример нескольких первых тетраэдрических чисел: 1, 4, 10, 20, 35, 56, 84, 120, 165, … . Формула для тетраэдрического числа: T n ( 4)=( n ( n +1)( n +2))/6.
Читать дальше





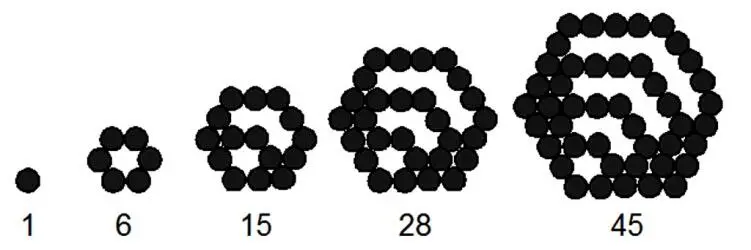

![Владимир Трошин - Княжич [СИ]](/books/404433/vladimir-troshin-knyazhich-si-thumb.webp)