Иэн Стюарт - Математические головоломки профессора Стюарта

123456789 × 10 = 1234567890;

123456789 × 11 = 1358024679;

123456789 × 12 = 1481481468;

123456789 × 13 = 1604938257;

123456789 × 14 = 1728395046;

123456789 × 15 = 1851851835;

123456789 × 16 = 1975308624;

123456789 × 17 = 2098765413;

123456789 × 18 = 2222222202;

123456789 × 19 = 2345678991.

В этих произведениях присутствуют все десять цифр 0–9 в некотором порядке, за исключением тех случаев, когда мы умножаем на число, кратное 3… Вплоть до 19, когда красивая закономерность останавливается (19 не кратно 3, но в ответе дважды встречается 9 и нет 0).

Но затем закономерность возобновляется:

Следующие исключения возникают на 28 и 29. На числах 30–36 все работает, на 37 вновь происходит сбой. На этом месте я прекратил вычисления. Что происходит дальше? Понятия не имею.

Сомс затянул узел до конца, сплющил его и поднес к свету.

– Вот это да, пятиугольник! – изумленно воскликнул я.

– Точнее сказать, Ватсап, это похоже на правильный пятиугольник, у которого одна диагональ видима, а остальные три скрыты. Обратите внимание на отсутствие горизонтальной диагонали. Если ее добавить, к примеру, сложив полоску еще раз, то получится…

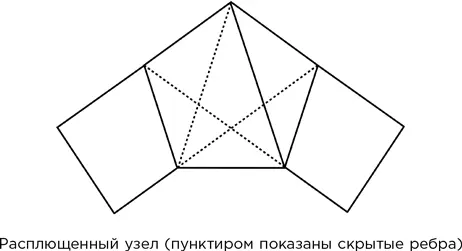
– Пятиконечная звезда! Пентаграмма! Ее используют в черной магии для вызова демонов!

Сомс кивнул.

– Но без этой последней складки и, соответственно, без одного ребра пентаграмма окажется неполной, и демон вырвется. Так что этот символ выражает угрозу выпустить в мир демонические силы, – он невесело улыбнулся. – Конечно, демонов в сверхъестественном смысле не существует, их невозможно ни вызвать, ни выпустить. Но вот люди демонического нрава, безусловно, существуют…

– Такие, к примеру, как в террористической организации Ал-Гебра! – воскликнул я. – Меня изгнали из Ал-Гебраистана оружием математического образования!

– Успокойтесь, Ватсап. Нет, я имел в виду скорее Матемагическую ассоциацию Нумерики. Это малоизвестная группа, и я сильно подозреваю, что она служит лишь официальным прикрытием для одной из дьявольских преступных схем Могиарти. Я сталкивался с ней и раньше, и теперь у меня в руках последнее, решающее звено, которое позволит нанести удар по зловещему профессору и навсегда разрушить эту часть его всемирной паутины преступлений. Если, конечно…

– Если что, Сомс?

– Если, конечно, мы сможем представить неопровержимые доказательства, когда дело дойдет до суда. Откуда мы знаем, что этот пятиугольник правильный?

– Но разве это не предельно просто?

– Напротив, вы скоро будете уверять меня, что это невероятно хитроумно и, может быть, вовсе не так, – хотя, говоря по существу, правильный ответ здесь совпадает с первой наивной догадкой. Осмелюсь предположить, что, как только мы установим этот факт, все остальное последует автоматически, но одного внешнего вида узла недостаточно. Однако я буду считать, что взаимное расположение линий на рисунке верно, так что у нас определенно есть пятиугольник с четырьмя диагоналями. Но действительно ли он правильный? В этом необходимо убедиться. Если это так, то этот факт должен следовать из постоянной ширины бумажной полоски. Обозначим углы так, как это делал великий Евклид из Александрии, и займемся геометрическими рассуждениями.

Я должен предупредить читателя, что остальная часть дискуссии будет интересна только тем, кто обладает некоторыми знаниями в евклидовой геометрии.

– Я начну, – объявил Сомс, – с нескольких простых наблюдений. Их можно доказать без большого труда с использованием базовой геометрии, так что подробности я опущу.

Во-первых, обратите внимание, что если две полоски, имеющие параллельные края, накладываются друг на друга, то в месте их перекрытия возникает ромб – параллелограмм, у которого все четыре стороны равны. Более того, если два таких ромба имеют одинаковую высоту и одинаковую сторону, то они конгруэнтны, то есть обладают одинаковыми размерами и формой. Следовательно, на диаграмме расплющенного узла присутствуют три конгруэнтных ромба.

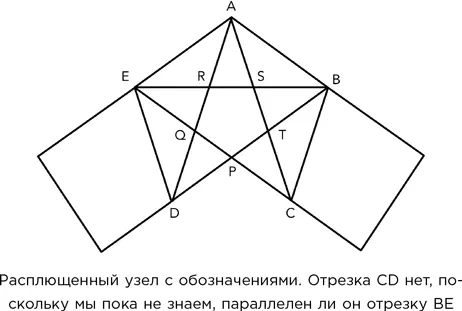
– Почему только три? – спросил я в недоумении.

– Потому что CD и BE не совпадают с краями бумажной полоски, так что мы не можем пока сказать то же о ромбах CDRB или DESC. Вот почему я не провел линии CD.