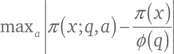Иэн Стюарт - Математические головоломки профессора Стюарта

Эти головоломки также исходят от Джерарда Баттерса, Фредерика Хенле, Джеймса Хенле и Колина МакГоги. См.: Gerard Butters, Frederick Henle, James Henle, and Colleen McGaughey. Creating clueless puzzles, The Mathematical Intelligencer 33 No. 3 (Fall 2011) 102–105.

– Вор – Волверстон, – объявил Сомс.

– Ты уверен, Хемлок? От твоей правоты многое зависит.

– Никаких сомнений быть не может, Спайкрафт. Вот их заявления:

Арбатнот: Это сделал Берлингтон.

Берлингтон: Арбатнот лжет.

Волверстон: Это не я.

Гамильтон: Это сделал Арбатнот.

Мы знаем, что кто-то один из этих людей говорит правду, а остальные трое лгут. Существует четыре возможных варианта. Рассмотрим их по очереди.

Если только Арбатнот говорит правду, то из его слов нам становится известно, что виновен Берлингтон. Однако в этом случае Волверстон лжет, следовательно, виновен именно Волверстон. Это логическое противоречие, делаем вывод о том, что Арбатнот не говорит правду.

– Если только Берлингтон говорит правду, то…

– Волверстон лжет! – воскликнул я. – Так что виновен Волверстон!

Сомс сердито взглянул на меня – ведь я сорвал его эффектное выступление.

– Это так, Ватсап, и остальные заявления этому не противоречат. Так что мы уже знаем, что вор – Волверстон. Однако имеет смысл проверить и остальные два варианта, чтобы избежать даже малейшей возможности ошибки.

– Все абсолютно ясно, дружище, – сказал я.

Сомс достал трубку, но не стал ее зажигать.

– Если только Волверстон говорит правду, то заявление Берлингтона ложно, следовательно, Арбатнот говорит правду. Снова противоречие, поскольку известно, что он лжет. Если только Гамильтон говорит правду, возникает это же противоречие. Поэтому единственный возможный вариант – тот, где правду говорит только Берлингтон, и тогда вор – Волверстон. Как Ватсап проницательно заметил.

– Благодарю вас, джентльмены, – сказал Спайкрафт. – Я знал, что могу на вас положиться.

По его жесту в комнату тенью проскользнула какая-то фигура. Короткий разговор шепотом, и человек вновь исчез.

– В жилище доктора будет немедленно проведен обыск, – сказал Спайкрафт. – Я уверен, что документ будет найден.

– Значит, мы спасли империю! – воскликнул я.

– До следующего раза, когда кто-нибудь оставит секретные документы на сиденье какого-нибудь кэба, – сухо заметил Сомс.

По пути домой я прошептал на ухо своему спутнику:

– Сомс, если Спайкрафт – специалист по простым числам, то что он делает в контрразведке? Ведь здесь не может быть никакой связи, правда?

Он внимательно посмотрел на меня и покачал головой. Что имелось в виду – отсутствие связи, о которой я говорил, или предупреждение и совет не развивать эту тему, – мне неизвестно.

123456 × 8 + 6 = 987654;

1234567 × 8 + 7 = 9876543;

12345678 × 8 + 8 = 98765432;

123456789 × 8 + 9 = 987654321.

Здесь не до конца ясно, что «должно» идти следующим: может быть,

234567890 × 8 + 10,

что равно 9876543130, так что закономерность на этом прекращается. Но, может быть, мне следовало взять (123456789) × 10 + 10 = 12345678900. Тогда

12345678900 × 8 + 10 = 9876543210.

Далее

(12345678900) × 10 + 11 = 123456789011,

что приводит нас к

12345689011 × 8 + 11 = 98765432099

и т. д. Если поэкспериментировать, можно поймать другую закономерность, которая продолжается до бесконечности.

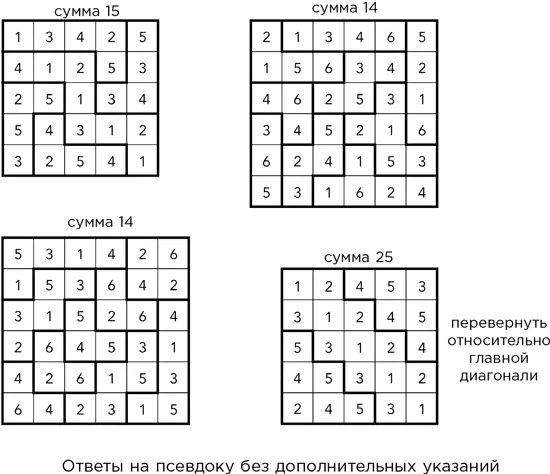
Гипотеза Эллиота – Халберстама [37] Peter Elliott and Heini Halberstam, A conjecture in prime number theory, Symposia Mathematica 4 (1968) 59–72. носит очень специальный характер. Пусть π ( x ) – число простых чисел, меньших или равных x . Для любого положительного целого q и a , не имеющего с q общих делителей, за исключением 1, пусть π ( x; q, a ) – число простых чисел, меньших или равных x и равных a (mod q ). Это приблизительно равно π( x ) / φ( q ), где φ – это пси-функция Эйлера, число целых чисел от 1 до q – 1, не имеющих с q общих делителей. Рассмотрим максимальную возможную ошибку:

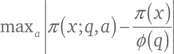
Гипотеза Эллиота – Халберстама говорит о том, насколько велика эта ошибка: гипотеза утверждает, что для любых θ < 1 и A> 0 существует постоянная C> 0 такая, что