Иэн Стюарт - Математические головоломки профессора Стюарта

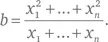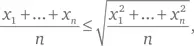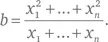
Я утверждаю, что для любых x j мы всегда имеем b>a , если только все x j не равны, в каковом случае b = a . Это следует из стандартного неравенства, связывающего среднее с тем, что инженеры называют «среднеквадратичным значением» (это корень квадратный из среднего значения квадратов):

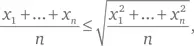
причем равенство достигается только при равенстве всех x j . Возведя в квадрат и сгруппировав, получим a за исключением случая равенства всех x j , что и требовалось. Дополнительную информацию можно найти на сайте

http://www.artofproblemsolving.com/wiki/index.php?title=Root-Mean_Square-Arithmetic_Mean-Geometric_Mean-Harmonic_mean_Inequality

Замечание Сомса – пример применения теории Рамсея – области комбинаторики, названной в честь Фрэнка Рамсея, доказавшего аналогичную, но более общую теорему в 1930 г. Его брат Майкл стал архиепископом Кентерберийским. Подойдем к нашему вопросу с осторожностью. Предположим, что некоторое число людей сидит за столом, причем каждый человек связан с другими либо ножом, либо вилкой. Выберем два произвольных числа f и k . Тогда существует некоторое число R , зависящее от f и k , такое, что если за столом присутствует по крайней мере R человек, то либо f из них соединены вилками, либо k – ножами.

Наименьшее такое R обозначается как R ( f, k ) и называется числом Рамсея. Из доказательства Сомса видно, что R (3,3) = 6. Числа Рамсея вычисляются с необычайным трудом, за исключением нескольких простых случаев. Известно, к примеру, что R (5,5) лежит в промежутке от 43 до 49, но его точное значение остается загадкой.

Рамсей доказал более общую теорему, в которой количество типов соединения (ножи, вилка, что угодно – чаще всего используются цвета, но Сомс использует то, что оказывается под рукой) может определяться любым конечным числом. Единственное известное нетривиальное число Рамсея для больше чем двух типов соединения – это R (3,3,3), равное 17.

Существуют бесчисленные обобщения этой идеи. Конкретное число, о котором идет речь, известно лишь в нескольких, очень немногочисленных, случаях. Вот статья, с которой все началось: F. P. Ramsey, On a problem of formal logic, Proceedings of the London Mathematical Society 30 (1930) 264–286. Как можно предположить по названию, автор думал о логике, а не о комбинаторике.

R. L. Graham and B. L. Rothschild, Ramsey theory, Studies in Combinatorics (ed. G.-C. Rota) Mathematical Association of America 17 (1978) 80–99.

В 1981 г. О. Свенсон опросил 161 шведского и американского студента, попросив каждого из них оценить свое мастерство и безопасность вождения по отношению к остальным участникам опроса. В отношении мастерства 69 % шведов оценили себя как выше среднего уровня; в отношении безопасности то же сделали 77 %. Для американских студентов цифры составили 93 % по мастерству и 88 % по безопасности. Мне довелось сдать два американских экзамена по вождению, один из которых проводился вообще без автомобиля, и я понимаю, почему американцы до такой степени преувеличивают свои способности. См.: O. Svenson, Are we all less risky and more skillful than our fellow drivers? Acta Psychologica 47 (1981) 143–148.

Тот же эффект наблюдается при оценке многих других качеств – популярности, здоровья, памяти, профессиональной квалификации, даже счастья в личной жизни. Не особенно удивительно: это один из способов поддержания самоуважения и уверенности в себе. А низкое самоуважение может быть признаком психологической неадекватности, поэтому, чтобы быть счастливыми и здоровыми, мы развили у себя в процессе эволюции способность к завышенной оценке собственного счастья и здоровья.

Не знаю, как вы, а я великолепно себя чувствую.

– Нужные нам числа – это 4 и 13, – сказал Сомс.

– Поразительно, просто поразительно. Я…

– Вы знакомы с моими методами, Ватсап.

– Тем не менее мне кажется замечательным, что вы можете вывести ответ из таких неопределенных разговоров.

– Хм. Посмотрим. Суть дела, Ватсап, состоит в том, что каждое утверждение, которое мы делаем, добавляет дополнительную информацию к тому, что знаем мы оба . И знаем , что оба знаем, и т. д. Предположим, что произведение двух нужных нам чисел равно p , а сумма равна s . Первоначально вы знаете p , а я знаю s . Мы оба знаем, что второй из нас знает то, что знает, но не знаем конкретного значения.