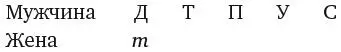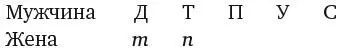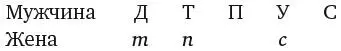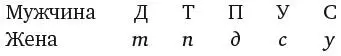Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Тезка кондуктора живет в Шеффилде, а нам известно, что мистер Джонс живет в Шеффилде. Стало быть, кондуктором должен быть Джонс. Как показано на рисунке ниже слева, мы можем отметить галочкой ячейку «Джонс – кондуктор», а также проставить крестики в других ячейках в той же строке и том же столбце, потому что у Джонса нет другой профессии, а остальные не являются кондукторами.

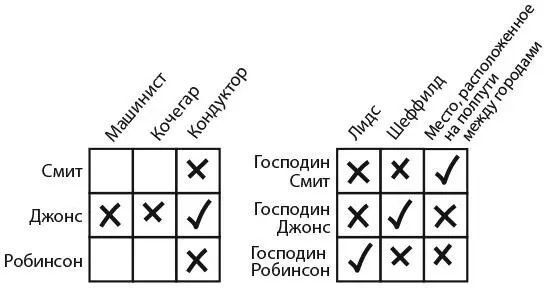
Подсказка о том, что Смит может выиграть у кочегара в бильярд, позволяет сделать вывод, что Смит не кочегар. (Кочегаром должен быть Робинсон.) Таким образом, мы ставим крестик в ячейке «Смит – Кочегар». Мы уже знаем, что Смит не кондуктор. Таким образом, методом исключения приходим к выводу, что Смит – машинист.

К тексту

Определить, кто из девочек ходил в кино, можно, перебрав всех по одной, каждый раз исходя из того, что данная девочка была в кинотеатре, и подсчитывая, сколько девочек лгут.

Предположим, в кино ходила Джоан Джаггинс. Ее утверждение о том, что это была Джоан Твигг, не соответствует действительности, как и утверждение Герти Гасс. Однако Бесси и Салли, должно быть, говорят правду. Когда мы отметим это в таблице, нам легче будет выявить закономерность. В первой строке представленной ниже таблицы отображена правдивость или ложность утверждений в случае, если Джоан Джаггинс была в кино, во второй строке – если в кино была Герти Гасс и т. д. В последнем столбце отображено общее количество ложных утверждений. Таким образом, если П – правда, а Л – ложь, первая строка начинается с последовательности Л, Л, П, П, а вся таблица выглядит следующим образом:

Если по меньшей мере семь утверждений не соответствуют действительности, значит, тайным киноманом должна быть Дороти Смит.

К тексту

Итак, у нас есть пять мужчин: Дженкинс, Томкинс, Перкинс, Уоткинс и Симкинс, для простоты – Д, Т, П, У и С. И есть пять женщин, которые являются матерями и женами конкретных мужчин, причем одна и та же женщина не может быть одновременно женой и матерью одного мужчины – любовь в Кинсдейле, конечно, странная, но не настолько. Давайте определим этих женщин по их родственным связям и обозначим эти связи строчными буквами: д – мать Д, т – мать Т и т. д.

Далее нарисуем таблицу, верхняя строка которой соответствует мужчинам, а нижняя – их женам, то есть сначала вторая строка пуста. Если Томкинс – пасынок Дженкинса, значит, миссис Дженкинс – мать Томкинса, поэтому можно вписать букву т под Д.

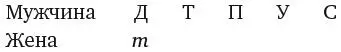
Нам также известно, что Томкинс – отчим Перкинса, а это значит, что миссис Томкинс – мать Перкинса. Следовательно, под Т пишем п.

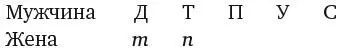
По условиям задачи, мать Перкинса – подруга миссис Уоткинс. Следовательно, мы знаем, что миссис Уоткинс не мать Дженкинса. Поскольку миссис Уоткинс не может быть матерью Уоткинса, методом исключения мы приходим к выводу, что она должна быть матерью Симкинса.

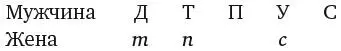
И наконец, сказано, что мать мужа миссис Уоткинс (то есть мать Уоткинса) – кузина миссис Перкинс. Следовательно, жена Перкинса не мать Уоткинса. Если жена Перкинса не мать Уоткинса, то она может быть только матерью Дженкинса. И снова методом исключения приходим к выводу, что жена Симкинса должна быть матерью Уоткинса.

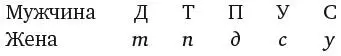
Таким образом, получается, что пасынок Симкинса – Уоткинс.

К тексту

Это табличная головоломка, поэтому рисуем таблицу. По условиям задачи, у нас есть пять домов и пять свойств, так что таблица должна выглядеть так, как показано ниже. Мы будем заполнять пустые ячейки, анализируя одно утверждение за другим.

Утверждение 9 гласит, что в среднем доме пьют молоко, поэтому мы можем записать слово молоко в третьем столбце. В утверждении 10 сказано, что датчанин живет в первом доме, значит, мы можем записать слово датчанин в первом столбце. Согласно утверждению 15, дом по соседству с домом датчанина синий, так что записываем слово синий во втором столбце.