Ю. Щербакова - Начертательная геометрия - конспект лекций

Проецирующие плоскости – это плоскости, которые перпендикулярны одной, и только одной, плоскости проекций.

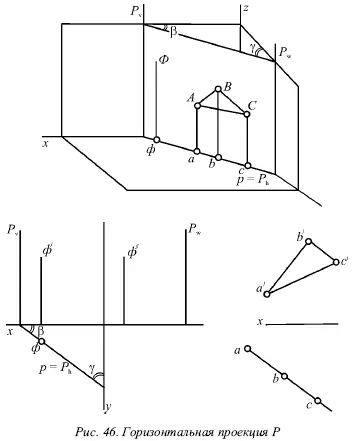
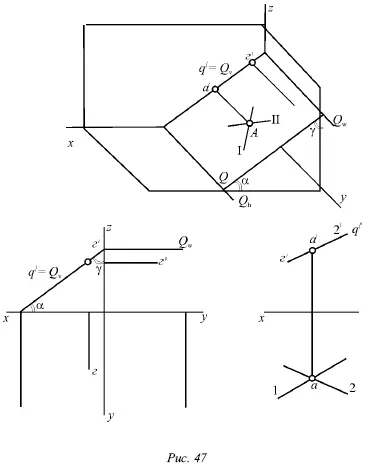
На рисунке 46 показана горизонтально-проектирующая плоскость Р , которая перпендикулярна горизонтальной плоскости; на рисунке 47 – фронтально-проектирующая плоскость Q , которая перпендикулярна фронтальной плоскости, и на рисунке 48 – профильно-проектирующая плоскость R, которая перпендикулярна профильной плоскости.

Среди свойств проецирующих плоскостей можно выделить следующие.

1. На одну из плоскостей проекций, т. е. на ту, которой данная плоскость перпендикулярна, эта плоскость проецируется в виде прямой линии. В этом случае говорят о проекции плоскости, подразумевая под ней именно эту прямую. Горизонтальнопроектирующая плоскость Р имеет горизонтальную проекцию р (рис. 46), фронтально-проецирующая плоскость Q – фронтальную проекцию q́ (рис. 47), а профильно-проецирующая R – профильную проекцию r˝ (рис. 48). Данные проекции совпадают с одноименными следами плоскостей, т. е. p = P h(рис. 46), q́ = Q v(рис. 47) и r˝ = R w(рис. 48).

2. Любая фигура, которая лежит в проецирующей плоскости, проецируется в виде отрезка прямой на плоскость проекций, перпендикулярную данной плоскости, т. е. треугольник ABC, который лежит в плоскости Р (рис. 46), имеет горизонтальную проекцию abc на горизонтальной проекции плоскости Р ( р = P h).

3. Фронтали горизонтально-проецирующей плоскости Р (рис. 47) перпендикулярны горизонтальной плоскости, а горизонтали фронтально-проектирующей плоскости Q (рис. 47) перпендикулярны фронтальной плоскости, т. е. перпендикулярность фронталей горизонтальной плоскости определяет горизонтально-проектирующую плоскость, а перпендикулярность горизонталей фронтальной плоскости является признаком фронтально-проектирующей плоскости. Профильно-проектирующая плоскость Р (рис. 47) имеет горизонтали, которые являются одновременно и фронталями; те и другие в этом случае перпендикулярны профильной плоскости.

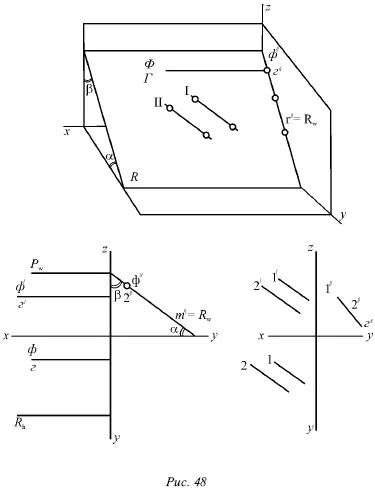
4. Горизонтально-проектирующая плоскость Р параллельна оси z , поэтому ее следы Р vи P wтакже являются параллельными оси z . Фронтально-проектирующая плоскость Q параллельна оси у , поэтому Q hи Q wпараллельны оси у. Профильно-проектирующая плоскость R параллельна оси х, и ее следы R hи R vпараллельны оси х . Третьи следы этих плоскостей, а именно P h, Q vи R w, способны занимать любое положение относительно осей проекций в зависимости от углов наклона этих плоскостей к плоскостям проекций.

5. Проектирующие плоскости с плоскостями проекции образуют углы, размеры которых видны на эпюре. На рисунках 46, 47 и 48 обозначен буквой угол между проектирующей плоскостью и горизонтальной плоскостью, буквой – угол с фронтальной плоскостью и буквой – с профильной плоскостью. Важно, что для данных плоскостей один из этих углов обязательно прямой, а два остальных угла составляют в сумме 90°. Данные два угла на эпюре равны углам, которые образуются следами плоскости с осями проекций.

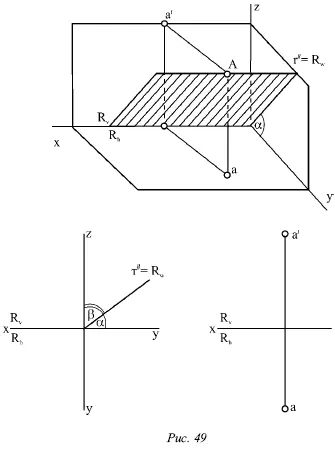
Рассмотрим плоскость, которая содержит ось х . Эта плоскость (рис. 49) принадлежит к числу профильно-проектирующих; она перпендикулярна профильной плоскости W , так как содержит ось х.

При этом горизонтальный и фронтальный следы R hи R vсливаются с осью х и не определяют положения плоскости R в пространстве. Для определения плоскости нужно дополнительно задать ее профильную проекцию r˝ ( r˝ = R w) (рис. 49) или указать положение какой-либо точки А на этой плоскости (рис. 49).

Для двух плоскостей возможны следующие варианты взаимного расположения: они параллельны или пересекаются по прямой линии.

Из стереометрии известно, что две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это условие называют признаком параллельности плоскостей.