Ю. Щербакова - Начертательная геометрия - конспект лекций

Через некоторую точку М можно провести огромное количество прямых, которые перпендикулярны данной прямой АВ . Они образуют целую плоскость Р , перпендикулярную АВ (рис. 34).

Из всех перпендикулярных прямых, которые при этом образуются, только одна пересекает данную прямую. Это прямая MN , которая проходит через точку N пересечения прямой АВ и плоскости Р .

Под перпендикуляром к прямой подразумевается прямая, не только перпендикулярная данной прямой, но и пересекающая в отличие от просто перпендикулярных скрещивающиеся прямые.

Прямой угол между скрещивающимися прямыми проецируется на данную плоскость проекций без искажения, если одна из прямых параллельна этой плоскости или лежит в ней.

Для произвольно расположенной плоскости проекции ее точек заполняют все три плоскости проекций. Поэтому не имеет смысла говорить о проекции всей плоскости целиком, нужно рассматривать лишь проекции таких элементов плоскости, которые ее определяют.

На основании законов стереометрии плоскость определяется, когда известны принадлежащие ей:

1) три точки, не лежащие на одной прямой;

2) прямая и точка, не находящаяся на этой прямой;

3) две пересекающиеся прямые;

4) две параллельные прямые.

Итак, плоскость будет считаться заданной, если имеется на эпюре одна из перечисленных выше комбинаций элементов, определяющих данную плоскость (рис. 35 случаи 1, 2, 3, 4).

Все четыре способа задания плоскости равнозначны, так как легко имея одну комбинацию элементов, изображенную на рисунке 35 перейти к любой другой.

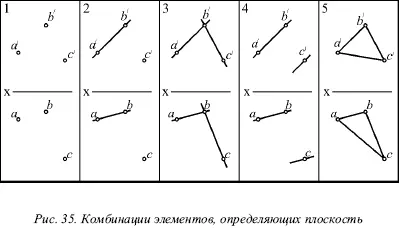
Если соединить одноименные проекции трех точек А, В и С , определяющих данную плоскость (рис. 35, случай 5), можно получить проекции треугольника ABC , лежащего в этой плоскости. Способ изображения плоскости в виде треугольника, не является принципиально новым, но обладает по сравнению с остальными четырьмя случаями большей наглядностью.

След плоскости Р – это линия пересечения ее с данной плоскостью или поверхностью (рис. 36).

Линию пересечения плоскости Р с горизонтальной плоскостью называют горизонтальным следоми обозначают P h, а линию пересечения с фронтальной плоскостью – фронтальным следоми обозначают Р v(рис. 37).

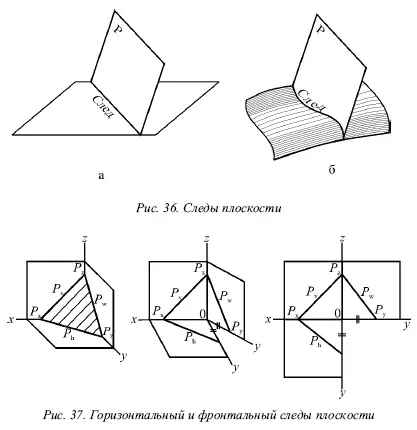
Иногда применяется и профильный след P w– линия пересечения данной плоскости с профильной плоскостью.

Точки, в которых пересекается плоскость Р с осями проекций, называют точками схода следов. Р х– точка схода следов на оси х, P у– на оси у , а Р z– на оси z (рис. 37). в точке Р пересекаются следы P hи P vи т. д.

Следы P hи P vплоскости Р являются прямыми, которые и лежат на горизонтальной и фронтальной плоскостях. Они имеют по одной из своих проекций, которые совпадают с осью х : горизонтальный след P h– фронтальную, а фронтальный P v– горизонтальную проекции.

Любую плоскость Р можно задать на эпюре с помощью указания положения двух ее следов – горизонтального и фронтального (рис. 38).

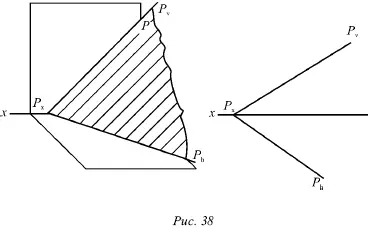
Следы P hи P vчаще всего изображаются парой пересекающихся или параллельных прямых и поэтому могут определять положение плоскости в пространстве.

Прямая принадлежит плоскости Р в том случае, если любые две ее точки лежат в данной плоскости.

Например, если следы прямой лежат на одноименных следах плоскости, то прямая лежит в этой плоскости (рис. 39).

Рассмотрим построение прямой, лежащей в данной плоскости Р .

Первый способ.Возьмем на следах P hи P vпо одной точке (рис. 40) и рассмотрим их как следы искомой прямой.

Рассматривая следы прямой, легко построить ее проекции.

Второй способ.Одну проекцию прямой, например горизонтальную 1, можно провести (рис. 40). Точки ее пересечения со следом P hи осью х определят горизонтальные проекции h и v следов искомой прямой. Если соединить прямой фронтальные проекции h́ и v́ следов, можно получить фронтальную проекцию 1́.