Ю. Щербакова - Начертательная геометрия - конспект лекций

Если две плоскости являются параллельными, то они пересекают какую-то третью плоскость по параллельным прямым. Исходя из этого у параллельных плоскостей Р и Q их следы являются параллельными прямыми (рис. 50).

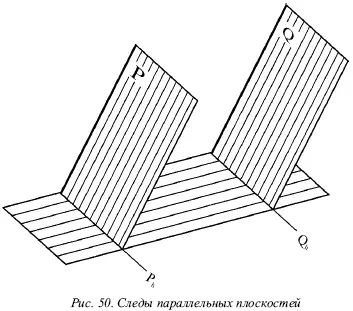
В случае, когда две плоскости Р и Q параллельны оси х , их горизонтальные и фронтальные следы при произвольном взаимном расположении плоскостей будут параллельными оси х, т. е. взаимно параллельными. Следовательно, при таких условиях параллельность следов является достаточным признаком, характеризующим параллельность самих плоскостей. Для параллельности подобных плоскостей нужно убедиться в параллельности и профильных их следов P wи Q w. Плоскости Р и Q на рисунке 51 параллельны, а на рисунке 52 они не параллельны, несмотря на то что P v|| Q v, и P hу || Q h.

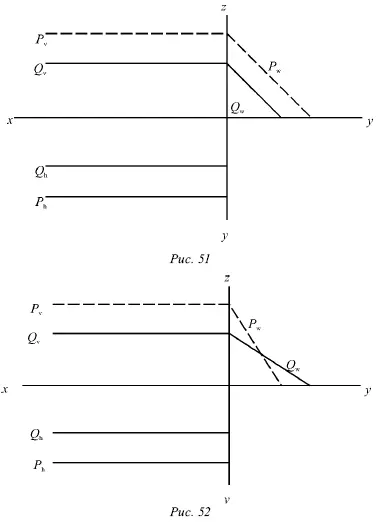
В случае, когда плоскости параллельны, горизонтали одной плоскости параллельны горизонталям другой. Фронтали одной плоскости при этом должны быть параллельными фронталям другой, так как у этих плоскостей параллельны одноименные следы.

Для того чтобы построить две плоскости, пересекающиеся между собой, необходимо найти прямую, по которой пересекаются две плоскости. Для построения этой прямой достаточно найти две точки, принадлежащие ей.

Иногда, когда плоскость задана следами, найти данные точки легко с помощью эпюра и без дополнительных построений. Здесь известно направление определяемой прямой, и ее построение основывается на использовании одной точки на эпюре.

Может быть несколько положений прямой относительно некоторой плоскости.

1. Прямая лежит в некоторой плоскости.

2. Прямая параллельна некоторой плоскости.

3. Прямая пересекает данную плоскость.

Рассмотрим признак параллельности прямой и плоскости. Прямая является параллельной плоскости, когда она параллельна любой прямой, лежащей в этой плоскости. На рисунке 53 прямая АВ параллельна плоскости Р , так как она параллельна прямой MN , которая лежит в этой плоскости.

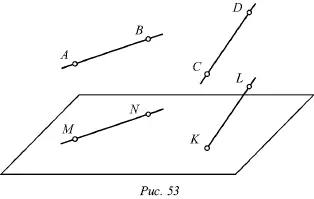
Когда прямая параллельна плоскости Р , в этой плоскости через какую-либо ее точку можно провести прямую, параллельную данной прямой. Например, на рисунке 53 прямая АВ параллельна плоскости Р . Если через точку М , принадлежащую плоскости Р , провести прямую NM , параллельную АВ , то она будет лежать в плоскости Р . На том же рисунке прямая CD не параллельна плоскости Р , потому что прямая KL , которая параллельна CD и проходит через точку К на плоскости Р , не лежит в данной плоскости.

Для нахождения точки пересечения прямой и плоскости необходимо построить линии пересечения двух плоскостей. Рассмотрим прямую I и плоскость Р (рис. 54).

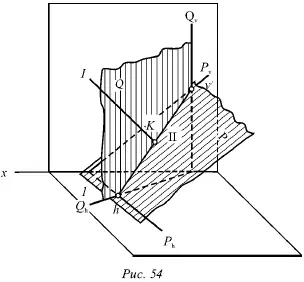
Рассмотрим построение точки пересечения плоскостей.

Через некоторую прямую I необходимо провести вспомогательную плоскость Q (проецирующую). Линия II определяется как пересечение плоскостей Р и Q . Точка К, которую и требуется построить, находится в пересечение прямых I и II. В этой точке прямая I пересекает плоскость Р .

В данном построении основным моментом решения является проведение вспомогательной плоскости Q , проходящей через данную прямую. Можно провести вспомогательную плоскость общего положения. Однако показать на эпюре проецирующую плоскость, используя данную прямую, проще, чем провести плоскость общего положения. При этом через любую прямую можно провести проецирующую плоскость. На основании этого вспомогательная плоскость выбирается проецирующей.

Прямая и плоскость перпендикулярны, если на плоскости можно найти две пересекающиеся прямые, перпендикулярные исходной прямой. В качестве подобной пары контрольных прямых легче всего рассматривать следы плоскости P hи P v(рис. 55). Это вызвано тем, что прямой угол между перпендикуляром к плоскости и следом P hдает проекцию на горизонтальную плоскость без искажения, а угол между перпендикуляром и следом Р vпроецируется на фронтальную плоскость V .