Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

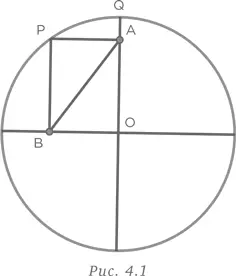
Эту задачу можно решить несколькими способами. Один из них — рассмотрение экстремумов. Предположим, что точка P на контуре круга совпадает с точкой Q . В этом случае отрезок AB должен совпадать с отрезком QO , который представляет собой радиус круга. Таким образом, площадь круга равна 144 π .

Задачу также можно решить, посмотрев на нее с другой точки зрения. Четырехугольник с тремя прямыми углами является прямоугольником. Отрезок AB — диагональ прямоугольника. PO также диагональ прямоугольника. Поскольку диагонали прямоугольника равны, радиус круга PO = 12, а площадь круга равна 144 π .

Стандартную колоду из 52 игральных карт делят случайным образом на две стопки по 26 карт в каждой. Как количество красных карт в одной стопке соотносится с количеством черных карт в другой?

При решении этой задачи, как правило, количество черных и красных карт в каждой стопке представляют следующим образом:

B1 = количество черных карт в стопке 1;

B2 = количество черных карт в стопке 2;

R1 = количество красных карт в стопке 1;

R2 = количество красных карт в стопке 2.

Поскольку общее количество черных карт равно 26, можно записать, что B1 + B2 = 26, а поскольку общее количество карт в стопке 2 равно 26, мы получаем R2 + B2 = 26.

Вычитание второго уравнения из первого, дает: B1 — R2 = 0. Таким образом, B1 = R2, т. е. количество красных карт в одной стопке равно количеству черных карт в другой. Хотя такое решение дает ответ, назвать его изящным нельзя. Наша цель в этой главе — найти такое решение, которое демонстрирует красоту и силу математики.

В качестве альтернативы возьмем все красные карты из стопки 1 и обменяем их на черные карты из стопки 2. Теперь все черные карты находятся в одной стопке, а красные — в другой. Таким образом, количество красных карт в одной стопке и количество черных карт в другой стопке должны быть равными. Задачу позволяет решить простая логика — нужно лишь взглянуть на эту задачу с другой точки зрения.

Лоэнгрину дали четыре отрезка цепи (рис. 4.2), в каждом из которых три звена. Покажите, как соединить эти четыре отрезка в замкнутую цепь, разомкнув и сомкнув не более трех звеньев.

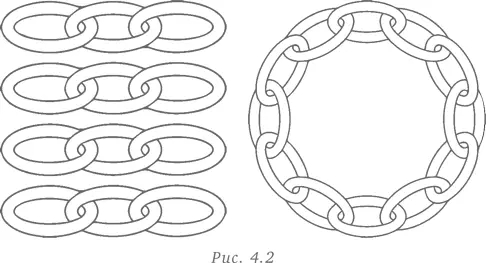
Обычно сначала пытаются разомкнуть последнее звено одного отрезка, присоединить его к другому отрезку и получить цепь из 6 звеньев. Затем размыкают звено третьего отрезка и присоединяют его к 6-звенной цепи, получая 9-звенную цепь. Присоединив последний отрезок к 9-звенной цепи, получают 12-звенную цепь, которая, однако, не является замкнутой . Таким образом, традиционный подход обычно завершается неудачей. Некоторые пробуют другие комбинации размыкания/замыкания звеньев каждого отрезка цепи, однако такой подход не приносит желаемого результата.

Эта задача хорошо решается с помощью стратегии принятия другой точки зрения. Можно даже сказать, что такой подход просто неоценим в данном случае. Вместо того, чтобы пытаться разомкнуть и замкнуть однозвено на каждом отрезке цепи , другая точка зрения предполагает размыкание всехзвеньев одного отрезка цепи и использование этих звеньев для соединения трех оставшихся отрезков цепи и получения требуемой замкнутой цепи. Это быстро приводит к правильному решению.

Какие натуральные числа менее 100 дают остаток 3 при делении на 7 и остаток 4 при делении на 5?

Рассмотрим ряд натуральных чисел менее 100, которые дают остаток 3 при делении на 7: {3, 10, 17, 24, 31, 38, 45, 52, 59, 66, 73, 80, 87, 49}. Теперь рассмотрим ряд натуральных чисел менее 100, которые дают остаток 4 при делении на 5: {4, 9, 14, 19, 24, 29, 34, 39, 44, 49, 54, 59, 64, 69, 74, 79, 84, 89, 94, 99}.

Сравнив эти два ряда, находим три совпадающих числа: 24, 59 и 94.

Попробуем взглянуть на эту задачу с другой точки зрения. Искомые числа должны иметь форму 7 n + 3, а также форму 5 k + 4, где n и k — целочисленные неизвестные. Объединим эти величины так, чтобы искать числа в форме 35 r + p , где r и p — целочисленные неизвестные. Первый ряд чисел, имеющих форму 7 n + 3, также можно представить, как 35 r + 3, 35 r + 10, 35 r + 17, 35 r + 24 и 35 r + 31. Только одно из этих чисел имеет также форму 5 k + 4, а именно 35 r + 24. Для того, чтобы узнать, какие числа менее 100, удовлетворяют этому соотношению, зададим r = 0, 1 и 2 и получим три искомых числа: 24, 59 и 94.