В день 1 она съела 1/2, значит было 16 печений.
Таким образом, вначале у Берты было 16 печений. Обратите внимание на то, что при вычислениях от обратного необходимо изменять используемые операции на «обратные». Вместо деления пополам мы должны удваивать, вместо сложения — вычитать и т. д. Это довольно легкий процесс.
Задача, которая ставит в тупик многих любителей математики, выглядит так: Марии 24 года. Она в два раза старше, чем была Анна, когда ей было столько же, сколько Анне сейчас. Сколько лет Анне?
Для решения этой задачи недостаточно просто составить уравнение, которое даст ответ. Требуется нечто большее. Можно начать с создания таблицы, показанной на рис. 3.4.

Мы имеем 24 = 2 a , следовательно a = 12. Кроме того, 24 − x = a + x = 12 + x , следовательно x = 6. Анне было 12, когда Марии было столько же (18), сколько Анне сейчас (18).
Подход от обратного может оказаться полезным для решения этой задачи. А раз так, то начнем со следующих рассуждений.
В представленной ситуации есть два временных периода:
1. Нынешнее время, когда Марии 24 года.
2. Прошлое время n лет назад.
Введем следующие обозначения:
M — возраст Марии (24), A — возраст Анны, n — разница между двумя временными периодами.
В первом временном периоде — Мария в два раза старше, чем была Анна:
2 ( A − n ) = M . (3.1)
Во втором временном периоде — когда Марии было столько же, сколько Анне сейчас:
M − n = A . (3.2)
Подставим уравнение 3.2 в уравнение 3.1:
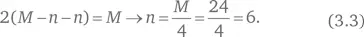
Значение n = 6 при подстановке в уравнение 3.2 дает:
M − 6 = A → A = 24 − 6 = 18.
Таким образом, возраст Анны составляет 18 лет.
От какой точки в выпуклом четырехугольнике сумма расстояний до каждой из вершин будет минимальной?
Большинство без особых раздумий пытаются методом проб и ошибок найти точку, для которой сумма расстояний до вершин будет наименьшей. Вполне возможно, что кто-то выберет точку на пересечении диагоналей. Это правильный ответ, однако такой подход оставляет вопросы.
Наша стратегия поиска ответа от обратного оказывается более рациональной в данном случае. Возьмем четырехугольник ABCD с диагоналями, пересекающимися в точке E , и с точкой P , которая, на наш взгляд, может быть искомой, имеющей минимальную сумму расстояний до вершин. Соединим точку P пунктирными линиями с вершинами, как показано на рис. 3.5.
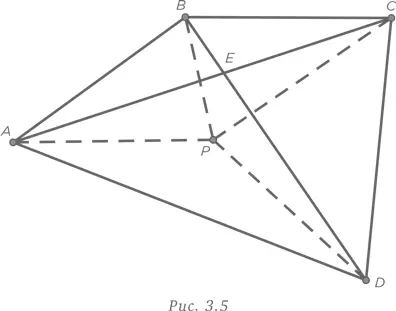
Рассмотрение треугольника APC показывает, что AP + PC > AC , поскольку сумма любых двух сторон треугольника всегда больше третьей стороны. Аналогичным образом, BP + PD > BD . В результате суммирования мы получаем, что AP + PC + BP + PD > AC + BD . Таким образом, отталкиваясь от предположения, что P может быть искомой точкой, мы находим, что выбор любой другой точки даст такой же результат. Единственной точкой, удовлетворяющей условиям задачи, является точка E на пересечении диагоналей.
Допустим, квадратные корни из уравнения x 2 + 3x — 3 = 0 равны r и s . Чему равна сумма r 2 + s 2 ?
Обычный подход заключается в решении уравнения для значений r и s . Используя формулу 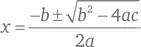 для определения корней квадратного уравнения вида ax 2+ bx + c = 0, мы получаем:
для определения корней квадратного уравнения вида ax 2+ bx + c = 0, мы получаем:
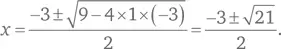
Теперь нам нужно найти квадраты этих корней и их сумму:
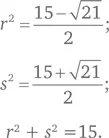
Чтобы получить более изящное решение, нужно вспомнить зависимость из элементарной алгебры, в соответствии с которой сумма корней квадратного уравнения ax 2+ bx + c = 0 составляет 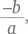 а произведение корней
а произведение корней 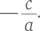 Из приведенного в условиях задачи уравнения мы находим, что сумма корней r + s = –3, а произведение rs = –3. При подходе от обратного, т. е. при определении суммы квадратов корней вместо прямых вычислений, как мы делали выше, для определения корней нам нужно искать эту сумму, поскольку ( r + s ) 2= r 2+ s 2+ 2 rs . Перепишем это уравнение следующим образом r 2 + s 2 = (r + s) 2 — 2rs .
Из приведенного в условиях задачи уравнения мы находим, что сумма корней r + s = –3, а произведение rs = –3. При подходе от обратного, т. е. при определении суммы квадратов корней вместо прямых вычислений, как мы делали выше, для определения корней нам нужно искать эту сумму, поскольку ( r + s ) 2= r 2+ s 2+ 2 rs . Перепишем это уравнение следующим образом r 2 + s 2 = (r + s) 2 — 2rs .
Читать дальше
Конец ознакомительного отрывка
Купить книгу


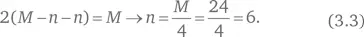

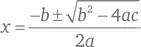 для определения корней квадратного уравнения вида ax 2+ bx + c = 0, мы получаем:
для определения корней квадратного уравнения вида ax 2+ bx + c = 0, мы получаем: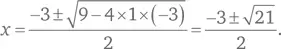
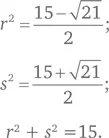
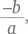 а произведение корней
а произведение корней 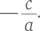 Из приведенного в условиях задачи уравнения мы находим, что сумма корней r + s = –3, а произведение rs = –3. При подходе от обратного, т. е. при определении суммы квадратов корней вместо прямых вычислений, как мы делали выше, для определения корней нам нужно искать эту сумму, поскольку ( r + s ) 2= r 2+ s 2+ 2 rs . Перепишем это уравнение следующим образом r 2 + s 2 = (r + s) 2 — 2rs .
Из приведенного в условиях задачи уравнения мы находим, что сумма корней r + s = –3, а произведение rs = –3. При подходе от обратного, т. е. при определении суммы квадратов корней вместо прямых вычислений, как мы делали выше, для определения корней нам нужно искать эту сумму, поскольку ( r + s ) 2= r 2+ s 2+ 2 rs . Перепишем это уравнение следующим образом r 2 + s 2 = (r + s) 2 — 2rs .










