Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Вместе с тем задачу можно решить более рационально при использовании подхода от обратного. В конечном итоге нам нужно получить 7 литров воды в 11-литровом сосуде, оставив свободным пространство объемом 4 литра. Откуда взялись эти 4 литра? (См. рис. 3.1.)

Чтобы получить 4 литра, мы должны оставить 1 литр воды в 5-литровом сосуде. Но как получить 1 литр в таком сосуде? Наполните 11-литровый сосуд водой и дважды отлейте воду в 5-литровый сосуд. В 11-литровом сосуде останется ровно 1 литр воды. Вылейте этот 1 литр в 5-литровый сосуд (рис. 3.2).

Теперь наполните 11-литровый сосуд и отлейте из него 4 литра воды в 5-литровый сосуд до его заполнения. В 11-литровом сосуде останутся требуемые 7 литров воды (рис. 3.3).

Учтите, что задачи подобного типа не всегда имеют решение. Иначе говоря, если вы хотите составить новую задачу такого вида, следует знать, что решение существует только в тех случаях, когда разница величин, кратных емкостям двух сосудов, может быть равной заданному объему. В нашем случае 2 × 11 − 3 × 5 = 7.

По определению, палиндром — это число, которое одинаково читается слева направо и справа налево. Так, числа 66, 595, 2332, 7007 являются палиндромами. Учитель Джека дал классу задание найти сумму первых 15 натуральных чисел. Джек взял калькулятор и сложил все числа от 1 до 15. Результат, к его удивлению, оказался палиндромом. Вместе с тем Джек пропустил одно число. Какое число он забыл включить?

Как правило пытаются составить все возможные комбинации слагаемых, исключая по одному числу каждый раз, до тех пор, пока сумма 14 чисел не даст палиндром. Такой грубый метод вполне работоспособен, особенно когда вы используете калькулятор. Вместе с тем он требует времени, если вы действительно исключаете по одному числу за раз.

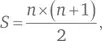Попробуем подойти к решению задачи иначе и сначала определим, какую сумму должны дать первые 15 натуральных чисел. Хотя можно воспользоваться известной формулой для вычисления суммы членов арифметической прогрессии, а именно намного интереснее пойти путем, который предложил Карл Фридрих Гаусс, когда ему было 10 лет. Вместо того, чтобы складывать числа последовательно: 1 + 2 + 3 + … + 14 + 15, он к первому числу прибавил последнее, затем ко второму — предпоследнее и т. д. В результате у него получилось семь раз по 16 и 8 в середине, что в сумме составило 7 × 16 + 8 = 120.

Поскольку Джек упустил одно слагаемое и получил палиндром, результатом должно быть число 111. Вы можете возразить, почему именно этот палиндром, а не 101, например? Чтобы получить 101, упустив одно число, вы должны забыть 19, а это число лежит за пределами нашего интервала 1–15. Таким образом, Джек забыл число 9.

Мама испекла печенье на полдник для Берты. В первый день Берта съела половину всего испеченного печенья. На второй день она съела половину от того, что осталось. На третий день — одну четверть остатка, а на четвертый — одну треть. На пятый день она довольствовалась половиной того, что осталось, а на шестой день доела одно последнее печенье. Какое количество печенья испекла мама Берты?

Первая реакция — написать ряд выражений, представляющих количество печенья, съеденного каждый день. Допустим, x — это начальное количество печенья.

Мама Берты испекла 16 печений.

Более эффективным является использование нашего подхода от обратного. Начнем с конца задачи и пойдем в обратном порядке:

В день 6 Берта съела одно последнее печенье, значит было 1 печенье;

В день 5 она съела 1/2, значит было 2 печенья;

В день 4 она съела 1/3, значит было 3 печенья;

В день 3 она съела 1/4, значит было 4 печенья;

В день 2 она съела 1/2, значит было 8 печений;