Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Таким образом, значение r 2 + s 2 = (–3) 2— 2 (–3) = 9 + 6 = 15.

Макс, Сэм и Джек играют в необычную карточную игру. В этой игре проигравший отдает другим игрокам столько денег, сколько у них есть. Макс проигрывает в первой партии и отдает Сэму и Джеку столько денег, сколько есть у каждого из них. Сэм проигрывает во второй партии и отдает Максу и Джеку столько денег, сколько есть у каждого из них. Джек проигрывает в третьей партии и отдает Максу и Сэму столько денег, сколько есть у каждого из них. На этом они решают закончить игру, и у каждого остается ровно $8,00. Сколько денег у каждого из игроков было перед началом игры?

Задача предполагает составление ряда уравнений, представляющих каждую партию. Обозначим начальную сумму денег у каждого игрока следующим образом: Макс — x , Сэм — y , Джек — z .

В последней партии, как мы знаем, каждое из значений равно 8. Это дает следующие три уравнения с тремя неизвестными:

В результате решения системы из трех уравнений мы получаем:

x = 13, y = 7, z = 4.

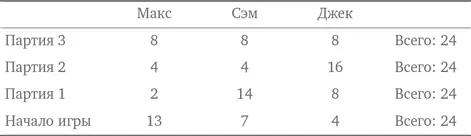
Обратите внимание, что в задаче дается конечная ситуация и спрашивается, какой была начальная ситуация. Это может указывать на эффективность подхода от обратного при решении. Также заметьте, что в соответствии с описанием ситуации в игре постоянно находится одно и то же количество денег (а именно $24). Подход от обратного дает изящное решение.

Макс начинает с $13, Сэм — с $7, а Джек — с $4. Ответ получился таким же, как и при обычном подходе, однако решение было более изящным.

Ал и Стив делят пятнистых саламандр для участия в выставке. Ал отбирает для своей экспозиции саламандр с двумя пятнами, а Стив — с семью пятнами. У Ала на пять саламандр больше, чем у Стива. Всего на их саламандрах 100 пятен. Сколько саламандр на двух экспозициях?

Характер этой задачи создает сложности для использования алгебры. Обычно количество саламандр у Ала обозначают как x , а количество саламандр у Стива — как y . Это позволяет составить следующие уравнения:

x — y = 5;

2 x + 7 y = 100.

Для решения этих двух уравнений умножим первое из них на 2:

2 x — 2 y = 10;

2 x + 7 y = 100.

Вычитание одного уравнения из другого дает следующий результат:

9 y = 90, или y = 10.

Теперь подставим значение y в первое уравнение и получим x = 15. Таким образом, у Ала и Стива вместе 15 + 10 = 25 саламандр. Это решение абсолютно правильное, но не самое изящное.

Посмотрим, можно ли упростить решение, использовав подход от обратного. Нас не спрашивают, сколько саламандр у каждого мальчика, мы должны определить сумму их саламандр. Поэтому можно начать с тех же двух уравнений. Иначе говоря, нам нужно найти x + y , а не значение каждой неизвестной. Составим те же два уравнения исходя из условий задачи.

x — y = 5;

2 x + 7 y = 100.

В этот раз, однако, будем искать способ определения суммы двух неизвестных.

Для этого умножим первое уравнение на 5, а второе на 2:

5 x — 5 y = 25;

4 x + 14 y = 200.

Теперь сложим эти два уравнения и получим 9 x + 9 y = 225 и x + y = 25. Такой метод необычен, но он демонстрирует более тонкий подход к решению задач, в которых требуется найти нечто иное, чем ожидают большинство людей.

Имея два следующих уравнения, найдите сумму x + y :

6 x + 7 y = 2007;

7 x + 6 y = 7002.

Традиционный подход заключается в решении двух уравнений с двумя неизвестными.

6 x + 7 y = 2007;

7 x + 6 y = 7002.

Умножим первое уравнение на 7, а второе на 6 и получим:

42 x + 49 y = 14 049;

42 x + 36 y = 42 012.

Вычтем одно уравнение из другого:

13 y = −27 963.

Таким образом, y = −2151.

Подставив это значение y в первое уравнение, мы получаем:

6 x − 15 057 = 2007;

6 x = 17 064;

x = 2844.

Таким образом, искомая сумма равна x + y = 2844 − 2151 = 693.