Генри Дьюдени - Пятьсот двадцать головоломок

Теперь давайте удалим отрезок AB . Тогда A и B станут четными узлами, а нам придется начинать и заканчивать наш маршрут в нечетных узлах D и x . Двигайтесь вдоль линии, показанной в случае 3 , и вы увидите, что это можно сделать, выбросив путь от A до B . Эту схему читатель легко преобразует в случай 4 , сказав себе: «Идем из x в D , из D в E , из E наружу и возвращаемся в E » и т. д. Маршрут можно изменить, соединив внешние мосты по-другому: принять за x внешний мост, идущий в A или B вместо D , и выбросить любой из путей AB , AD , BD , xA , xB или xD . В случае 5 путь из x идет в B . Мы по-прежнему выбросили AB , но должны теперь начинать и заканчивать движение в D и x . Преобразовав эту диаграмму (см. случай 6 ), можно заметить, что получился тот же самый чертеж, который я приводил, формулируя задачу. Теперь читатель может начертить столько маршрутов, сколько пожелает, но при этом всегда придется удалять один из путей (мостов). На примере нашей головоломки хорошо видно, как некоторая изобретательность (вроде той, что была проявлена при преобразовании диаграмм) помогает нащупать правильный подход.

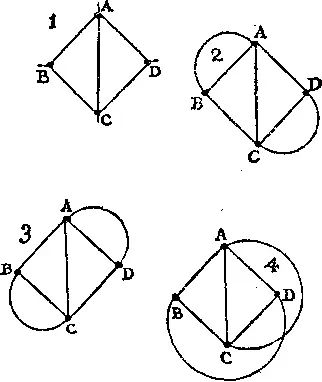
404. Преобразуйте карту следующим образом. Сведите острова A , B , C и D просто к точкам, а мосты превратите в линии, как это сделано в случае 1 . Условия задачи от этого не меняются. Если вы соедините A и B , а также C и D линиями, которые будут проходить вне четырехугольника ABCD , то получите случай 2 ; если же вы подобным образом соедините A и D , а также B и C , то получите случай 3 ; если же вы соедините A с C , а B с D , то получите случай 4 . В каждом из этих случаев B и D представляют собой «нечетные узлы» (точки, из которых можно выйти по нечетному числу путей, а именно по трем путям), так что при любом маршруте вы должны начинать и заканчивать свой путь в В или D для того, чтобы пройти один и только один раз вдоль каждой линии. Следовательно, Томпкинс обязан жить в B или D . Для определенности мы положим, что он живет в B , и поместим Джонсона в D . Всего существует 44 маршрута в случае 2, 44 в случае 3 и 44 в случае 4, что составляет всего 132 маршрута, если мы не различаем маршруты с противоположным направлением обхода. Возьмем, например, случай 2 и обозначим внешние кривые линии через O . Тогда, если вы начнете движение по BOAB , BOAC , BAOB или BAC , каждый из этих вариантов даст по 6 различных маршрутов. Если вы начнете движение по BOAD , BAD , BCOD , BCA или BCD , то получите по 4 маршрута. В случае 3 BOCA , BOCB , BCA или BCOB дадут по 6 маршрутов, a BOCD , BAOD , BAC , BAD или BCD — по 4 маршрута каждый. Аналогичным образом обстоит дело и в случае 4 .

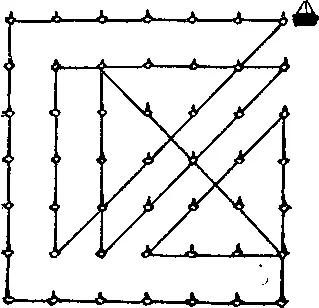
405. На рисунке показано, каким образом военный корабль может потопить 49 судов за 12 прямых курсов, закончив движение в той же точке, откуда начал. Двигайтесь вдоль каждой прямой до того места, где он меняет направление.

[Доказано, что можно соединить все точки, расположенные в виде квадрата n × n , непрерывным путем, состоящим из 2 n - 2 отрезков прямой, для всех n > 2. Случай n = 3 представляет собой хорошо известную головоломку, которую большинству решить не удается, поскольку те, кто решает, не всегда догадываются продолжить отрезки за пределы квадрата. 5 × 5 — это наименьший квадрат, в котором линия из 2 n - 2 отрезков может не выходить за его пределы.

Можно построить замкнутый путь (у такого пути концы совпадают, как в приведенной выше головоломке) из 2 n - 2 отрезков для всех квадратов со стороной, большей 3. Квадрат 7 × 7 представляет собой наименьший квадрат с нечетной стороной, для которого существует замкнутый путь из 2 n - 2 отрезков, не выходящий за пределы данного квадрата. (Наименьший квадрат с четной стороной, для которого можно нарисовать подобный путь, равен 6 × 6.)

Приведенное здесь Дьюдени решение имеется в книге Сэма Лойда «Cyclopedia of Puzzles» как решение одной из его головоломок. Лойд говорит, что он впервые опубликовал эту головоломку в 1908 г., и отзывается о данном решении как об «удивительно трудном трюке». Позаимствовал ли Лойд свою головоломку у Дьюдени или наоборот, еще не установлено.