Обратите внимание на то, что это решение для случая 7 × 7 является одновременно решением задачи о замкнутом «пути ферзя» на шахматной доске 7 × 7 за 2 n - 2 ходов. Замкнутый путь ферзя за 2 n - 2 ходов возможен также на любой доске со сторонами, большими 7. Замкнутый путь ферзя за 14 ходов на обычной доске 8 × 8 был впервые найден Сэмом Лойдом, который считал эту задачу одной из лучших своих головоломок.
Число 2 n - 2 является необходимым также для любой квадратной доски. — М. Г. ]
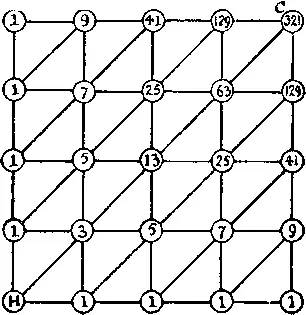
406. Из дома H до любой из точек, расположенных к северу или к востоку от него, можно добраться лишь одним путем. Поэтому я в этих точках поставил цифру 1 . Теперь возьмем второй столбец и заметим, что существуют 3 пути, ведущие во вторую снизу точку, 5 — в следующую, 7 — в следующую за ней и т. д., причем при переходе в очередную расположенную выше точку число путей увеличивается на 2. То же самое применимо и ко второй снизу строке. Выпишем везде соответствующие цифры. Далее, до центральной точки можно добраться 13 путями, поскольку мы можем к ней подойти или из точки снизу (5 путей), или из точки слева (5 путей), или из точки слева внизу по диагонали (3 пути), что в сумме и даст 13 путей. Таким образом, все, что нам осталось сделать,- это выписывать по очереди в каждой точке сумму трех чисел, расположенных в ближайших точках, из которых можно непосредственно попасть в данную. Отсюда мы и получим, что общее число путей, ведущих из H в C , равно 321.
407. На рисунке показано, как лучше всего разрезать сеть. Нетрудно видеть, что 8 разрезов от A до B делят сеть на 2 части.

408. Можно заметить, что каждый участок соединен с остальными четным числом мостов (2, 4 или 6); исключение составляют участки C и L , в которые ведут по 3 моста (нечетное число). Следовательно, чтобы пройти по каждому мосту один и только один раз, необходимо начинать и заканчивать маршрут в C и L , где как раз и расположены дома наших двух приятелей. Так, отправляясь из C , мы можем двигаться по следующему маршруту: C , G , F , C , B , A , D , H , E , I , H , J , K , L , M , G , I , F , B , E , F , I , L .
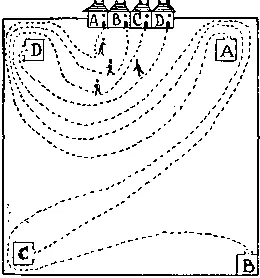
409. Решение ясно из рисунка.
410. Фразу HERE LIES JOHN RENIE можно прочитать 45 760 способами (или, если разрешается перемещаться от одной буквы к следующей и по диагонали, 91 520 способами), поскольку, добравшись до углового I, мы обязаны сместиться назад по диагонали к ближайшему Е. За недостатком места здесь не приводятся детали решения. Единственная дополнительная информация о камне заключается в окончании фразы: «...который умер 31 мая 1832 г. в возрасте 32 лет».

411. На рисунке показан путь, удовлетворяющий всем заданным условиям.
412. Наикратчайший путь в ABCHCDEIEFGBHDIHGIFAG . Таким образом, инспектор проделает путь в 211 км, проехав по двум коротким дорогам CH и EI дважды.
413. Существует 2501 маршрут от B до D , а именно:
| Количество |
Число |
Число |
|
| участков |
маршрутов |
вариаций |
|
| 1 |
1 |
2 |
2 |
| 2 |
1 |
9 |
9 |
| 3 |
2 |
12 |
24 |
| 4 |
5 |
18 |
90 |
| 5 |
4 |
72 |
288 |
| 6 |
14 |
36 |
504 |
| 8 |
22 |
72 |
1584 |
|
|
|
2501 |
Достаточно рассмотреть маршруты от B до D . Маршрут, состоящий из 1 участка, ведет прямо в D . Маршрут из 2 участков есть CD . Маршрутами из 3 участков будут CBD и DCD . Пятью маршрутами из 4 участков являются DBCD , DCBD , CBCD , CDCD и CDBD . У каждого из этих маршрутов есть вариации, связанные с выбором конкретных участков, и число таких вариаций одинаково для любого маршрута, содержащего данное количество участков. Маршрутов с семью участками не существует.
414. Число различных путей равно 264. Эта головоломка довольно трудна, но недостаток места не позволяет мне показать наилучший метод подсчета всех маршрутов.
415. Существует 60 маршрутов, следуя по которым миссис Симпер могла бы посетить каждый город по одному и только по одному разу, закончив путь в H , если считать различными маршруты, отличающиеся только направлением. Однако если леди должна избежать тоннелей между N и O , а также между S и R , то можно обнаружить, что число различных маршрутов сокращается до 8.
Читать дальше











![О Генри - Через двадцать лет [After Twenty Years]](/books/415401/o-genri-cherez-dvadcat-let-after-twenty-years-thumb.webp)

