Генри Дьюдени - Пятьсот двадцать головоломок

425. Расположите 16 монет в виде квадрата 4 × 4. Затем положите по одной монете сверху на первую монету первой строки, на третью монету второй, на четвертую — третьей и на вторую — четвертой строки.

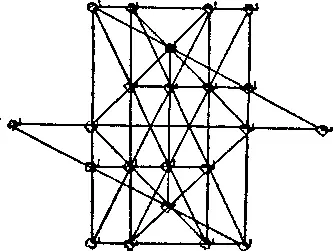
426. На рисунке показано, как следует пересадить 6 деревьев, чтобы получилось 20 рядов по 4 дерева в каждом.

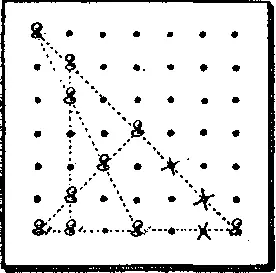
427. На рисунке показано, как следует расположить колышки. Три колышка из дырок, отмеченных крестиками, надо поместить в левый верхний угол. После этого 10 колышков образуют 5 рядов по 4 колышка в каждом. Если вы отразите диаграмму в зеркале, то получите единственное решение, отличное от данного.

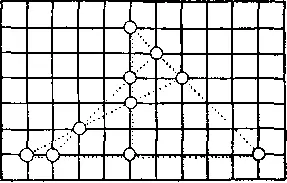
428. Решение показано на рисунке. Десять фишек образуют 5 прямых по 4 фишки на каждой.

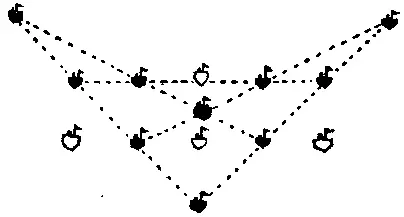
429. На рисунке видно, что корабли образуют 5 прямых по 4 корабля на каждой, а белые призрачные корабли указывают позиции, с которых 4 из них были перемещены.

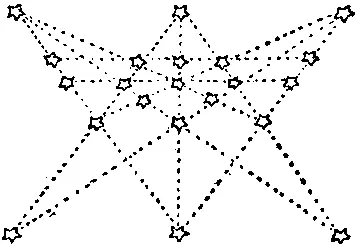
430. На рисунке представлено симметричное решение, при котором 21 звезда образует 11 прямых по 5 звезд на каждой прямой.

431. Очевидно, что для двух и большего числа прилегающих стран необходимы по крайней мере две краски (случай 1 ). Если три страны попарно прилегают друг к другу, то необходимы три краски (случай 2 ). Для четырех стран требуются три краски, если четвертая ( Ж ) страна прилегает к двум другим, уже прилегающим друг к другу (случай 3 ). (Поскольку возможен вариант, когда, как в случае 4 , краска 3 прилегает к двум не прилегающим друг к другу странам, и в силу этого можно обойтись двумя красками.) Четыре же краски понадобятся и в случае, когда четвертая страна прилегает к каждой из трех прилегающих друг к другу стран (случай 5 ).

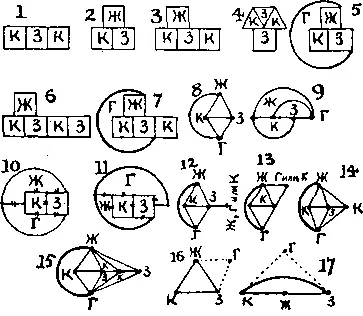
Для пяти прилегающих стран потребуются 3 краски, если одна страна прилегает к двум прилегающим друг к другу странам (случай 6 ). Четыре краски потребуются, если пятая страна прилегает к каждой из трех прилегающих друг к другу стран (случай 7 ). Однако 5 красок потребовались бы в случае, если бы пятая страна прилегала к четырем прилегающим друг к другу странам. Если такая карта возможна, то теорема не верна.

Рассмотрим сначала четыре страны, прилегающие друг к другу. Мы произведем небольшое преобразование, приняв, что любые две прилегающие друг к другу страны связаны между собой мостом. Мост может иметь любую длину, а страны можно свести просто к точкам, не влияя на условия [41] См. решение задачи 403. — Прим. перев. . В случаях 8 и 9 я изобразил четыре страны (точки), соединенные между собой мостами (линиями). Относительное расположение этих точек совершенно несущественно, и выясняется, что в каждом возможном случае к одной из стран (точек) нельзя подобраться снаружи.

Это легко доказать. Если 3 точки связаны между собой прямыми, то эти точки должны либо образовывать треугольник, либо лежать на одной прямой. Предположим сначала, что они образуют треугольник ЖКЗ , как в случае 16 . Тогда четвертая страна ( Г ) должна лежать либо внутри треугольника, либо вне его. Если она лежит внутри, то очевидно, что она окружена. Поместим ее снаружи и соединим с Ж и З , как показано на рисунке; тогда Г нельзя соединить с К , не окружив при этом Ж или З . Пусть Г прилегает к Ж или К ; тогда Г нельзя соединить с З , не окружив либо Ж , либо К . Пусть Г прилегает к К и З ; тогда Г нельзя соединить с Ж , не окружив либо Ж , либо З .

Рассмотрим теперь второй вариант, когда КЖЗ лежат на прямой (случай 17 ). Если Г лежит внутри, то она окружена. Поместим Г снаружи и соединим, как показано, с К и З ; тогда Г нельзя соединить с Ж , не окружив при этом либо К , либо З . Пусть Г прилегает к К и Ж ; тогда Г нельзя соединить с З , не окружив К или Ж . Пусть Г прилегает к Ж и З ; тогда Г нельзя соединить с К , не окружив Ж или З .