396. Вместимость кувшина должна быть чуть меньше 3 л. Точнее говоря, она равна 2,93 л.
397. Две пинты воды можно отмерить за 14 операций, если сосуды над чертой пусты, а каждая строка соответствует одной операции.
| 7 л |
11 л |
| 7 |
0 |
| 0 |
7 |
| 7 |
7 |
| 3 |
11 |
| 3 |
0 |
| 0 |
3 |
| 7 |
3 |
| 0 |
10 |
| 7 |
10 |
| 6 |
11 |
| 6 |
0 |
| 0 |
6 |
| 7 |
6 |
| 2 |
11 |
|
Содержимое сосудов, указанное после каждой операции, не требует пояснений.
398. Смесь содержит вина и воды.
399. Вот одно из нескольких решений:
| Емкость сосудов в унциях |
24 |
13 |
11 |
5 |
| Содержимого в сосуде: |
|
|
|
|
| до переливания |
24 |
0 |
0 |
0 |
| после 1-го переливания |
0 |
8 |
11 |
5 |
| после 2-го переливания |
16 |
8 |
0 |
0 |
| после 3-го переливания |
16 |
0 |
8 |
0 |
| после 4-го переливания |
3 |
13 |
8 |
0 |
| после 5-го переливания |
3 |
8 |
8 |
5 |
| Итого |
8 |
8 |
8 |
0 |
|
[Найдено лучшее решение, содержащее только 5 операций:
| 8 |
0 |
11 |
5 |
| 8 |
11 |
0 |
5 |
| 8 |
13 |
3 |
0 |
| 8 |
8 |
3 |
5 |
| 8 |
8 |
8 |
0 — М. Г. ] |
400. Простейшим решением задачи будет следующее (вверху указана емкость сосудов, ниже — первоначальное количество содержимого, а в каждой следующей строке — количество содержимого после очередной операции):
| 80 л |
80 л |
5 л |
4 л |
| 80 |
80 |
0 |
0 |
| 75 |
80 |
5 |
0 |
| 75 |
80 |
1 |
4 |
| 79 |
80 |
1 |
0 |
| 79 |
80 |
0 |
1 |
| 74 |
80 |
5 |
1 |
| 74 |
80 |
2 |
4 |
| 78 |
80 |
2 |
0 |
| 78 |
76 |
2 |
4 |
| 80 |
76 |
2 |
2 |
|
Так, мы сначала наполняем 5-литровый кувшин из одного бидона, затем 4-литровый кувшин из 5-литрового, затем выливаем содержимое 4-литрового обратно в бидон и т. д. Все это можно проделать очень легко. Обратите внимание на остроумие последних двух операций: мы наполняем 4-литровый кувшин из второго бидона, а затем доверху доливаем первый бидон.
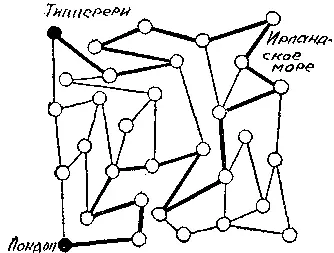
401. Жирная линия на рисунке показывает путь из Лондона в Типперери, совершаемый за 18 переходов. Чтобы добраться до места назначения за четное число переходов, совершенно необходимо включить в маршрут переход, отмеченный словами Ирландское море.

402. Десять точек, отмеченных на рисунке буквами, представляют собой «нечетные узлы», то есть точки, из которых вы можете идти по нечетному числу (три) направлений. Следовательно, нам известно, что всего потребуется 5 линий (половина 10). Пунктирные линии показывают 4 кратчайших расстояния между узлами. Обратите внимание, что вам нельзя использовать один узел дважды; в противном случае решение можно было бы удушить, обозначив пунктиром EH и CF вместо CD и GH . Зафиксировав наши 4 кратчайших расстояния, мы можем начертить все остальное с помощью одной непрерывной линии от A до K , как показано на рисунке. Добравшись до D , вы должны пройти к C и обратно к D , от G к H и обратно и т. д. Или же вы можете подождать до того момента, когда доберетесь до C , а затем пройти до D и обратно и т. д. Таким образом, вы пройдете дважды только пунктирные линии, что и даст минимально возможное расстояние, которое приходится проходить дважды.
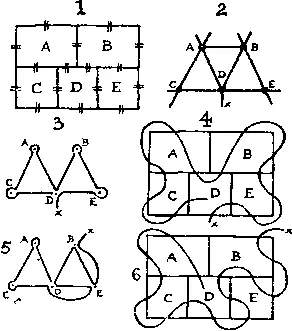
403. Допустим, что мы пересекаем отрезки по мостам, изображенным в случае 1 маленькими параллельными линиями. Далее я преобразую диаграмму, сведя области A , B , C , D , E просто к точкам и изобразив мосты, связывающие данные точки, прямыми, или путями, — случай 2 . При этом никакого изменения условий не произошло, поскольку в каждом случае имеется 16 мостов (путей) и они связывают A , B , C , D , E совершенно одинаковым образом. Можно заметить, что наружу выходят 9 мостов, или путей. Очевидно, мы можем попарно соединять данные пути, заботясь лишь о том, чтобы они не пересекали друг друга. Простейший способ показан в случае 3 . Выйдя из A , B , C или E , мы немедленно возвращаемся в ту же точку по соседнему мосту, оставив одну точку x обязательно вовне. В случае 2 имеются 4 нечетных узла A , B , D и x (если мы решили входы и выходы сделать такими, как в случае 3 ); поэтому, как я уже объяснял, нам потребуется 2 росчерка (половина 4), чтобы пройти по всем путям, откуда и следует неразрешимость нашей задачи.
Читать дальше










![О Генри - Через двадцать лет [After Twenty Years]](/books/415401/o-genri-cherez-dvadcat-let-after-twenty-years-thumb.webp)

