У 6 из 37 решений сумма вершин равна 26, а именно:
| 10 |
6 |
2 |
3 |
1 |
4 |
7 |
9 |
5 |
12 |
11 |
8 |
| 9 |
7 |
1 |
4 |
3 |
2 |
6 |
11 |
5 |
10 |
12 |
8 |
| 5 |
4 |
6 |
8 |
2 |
1 |
9 |
12 |
3 |
11 |
7 |
10 |
| 5 |
2 |
7 |
8 |
1 |
3 |
11 |
10 |
4 |
12 |
6 |
9 |
| 10 |
3 |
1 |
4 |
2 |
6 |
9 |
8 |
7 |
12 |
11 |
5 |
| 8 |
5 |
3 |
1 |
2 |
7 |
10 |
4 |
11 |
9 |
12 |
6 |
Первое решение представлено на рисунке II , а предпоследнее — на рисунке III , так что, обратившись к рисунку, вы поймете, как следует располагать эти числа на звезде. Читателю следует все приведенные выше решения изобразить на звезде и помнить, что вместо 6 вместе с дополнительными получится 12 решений. Первые четыре решения будут регулярного, а последние два — нерегулярного типа. Если читатель попытается найти все 37 (или 74) решений данной головоломки, то ему будет полезно знать, что существует соответственно 3, 6, 2, 4, 7, 6, 9 (всего 37) решений с суммой вершин, равной 24, 26, 30, 32, 34, 36, 38.
[Для шестиконечной звезды существует 80 решений. — М. Г. ]
385. Поместите 5 в верхний кружок. Затем расположите четыре числа (7, 11, 9, 3) на горизонтальной линии так, чтобы сумма внешних чисел равнялась 10, а внутренних 20 и чтобы разность между двумя внешними числами в два раза превышала разность между двумя внутренними числами. Затем поместите числа, дополняющие их до 15, в соответствующие кружочки, как показано пунктирными линиями. Остальные четыре числа (13, 2, 14, 1) расставить уже легко. Из этого основного размещения мы можем получить три остальных: первое — поменяйте местами 13 с 1, а 14 с 2; второе и третье — подставьте в полученных двух размещениях вместо каждого числа разность между ним и 15 (например, 10 вместо 5, 8 вместо 7, 4 вместо 11 и т. д.). Следуя этим правилам, читатель может сам построить вторую группу из четырех решений.

Общее решение слишком длинно, чтобы приводить его здесь полностью, однако существует всего 56 различных размещений (вместе с дополнительными). Я разбиваю их на три класса. В класс I включаются все случаи, подобные приведенным выше, где пары в положениях 7—8, 13—2, 3—12, 14—1 в сумме дают 15, а всего таких случаев 20. В класс II включаются случаи, в которых пары в положениях 7—2, 8—13, 3—1, 12—14 в сумме дают 15; таких случаев снова 20. В класс III входят все случаи, в которых пары в положениях 7—8, 13—2, 3—1, 12—4 в сумме дают 15; таких случаев 16. Всего получается 56 случаев.
[Для семиконечной звезды существует 72 решения. — М. Г. ]
386. На рисунке приведено искомое решение. Сумма четырех чисел вдоль любой прямой равна 34. Если решение для одной звезды известно, то его можно без труда преобразовать в решение для второй звезды, отметив, как перемещаются числа в приведенных двух решениях.
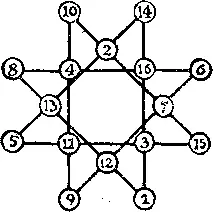
Мне не удалось подсчитать общее количество решений для звезд данного порядка. Это, как мне кажется, весьма трудная задача. Быть может, читатели попытают в ней счастья.
[Для случая восьмиконечной звезды известно 112 различных решений. — М. Г. ]
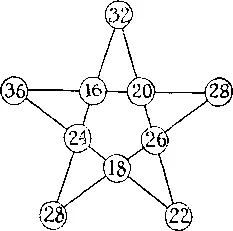
387. На рисунке показан один из способов размещения гарнизонов, при котором общее число солдат вдоль каждой из пяти линий равно 100.
388. Положите карты 1, 2, 3, 4, 5 в последовательности, показанной пунктирными линиями, то есть каждую следующую карту помещайте через один угол, двигаясь по часовой стрелке, а затем разместите в противоположном направлении карты 6, 7, 8, 9, 10, позаботясь о том, чтобы 6 было расположено с нужной стороны от 5. Сумма очков на каждой стороне равна 14. Если вы теперь разместите карты 6, 7, 8, 9, 10 первым способом, а карты 1, 2, 3, 4, 5 вторым, то получите другое решение — с суммой, равной 19. Теперь проделайте то же самое о двумя множествами чисел 1, 3, 5, 7, 9 и 2, 4, 6, 8, 10, и вы получите еще два решения с суммами соответственно 16 и 17.
Всего существует 6 решений, из которых 2 последних являются особыми. Выпишите в том же порядке 1, 4, 7, 10, 13 и 6, 9, 12, 15, 18; выпишите также 8, 11, 14, 17, 20 и 3, 6, 9, 12, 15. Затем вычтите 10 из каждого числа, большего 10.
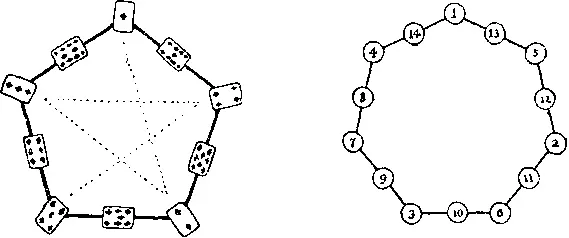
389. Решение вы видите на рисунке справа. Начав с верхнего кружка и двигаясь по часовой стрелке, вписывайте числа от 1 до 7 через одну вершину. Затем, начав сразу над 7 и двигаясь в противоположном направлении, заполните свободные места числами от 8 до 14. Если же вы сначала впишите числа 1, 3, 5, 7, 9, 11, 13, а затем 2, 4, 6, 8, 10, 12, 14, то получите другое решение с суммой 22 вместо 19. Если в приведенных решениях заменить каждое число разностью между ним и 15, то получатся два дополнительных решения с суммами, равными соответственно 26 и 23 (разность между 45 и 19, 45 и 22).
Читать дальше











![О Генри - Через двадцать лет [After Twenty Years]](/books/415401/o-genri-cherez-dvadcat-let-after-twenty-years-thumb.webp)

