Чтобы построить прямую, по которой плоскость сечения пересечет нижнее основание куба (эта прямая называется следом ), нужно знать две точки, принадлежащие этой прямой. Одна точка нам дана — это точка R . Другую точку найдем, если продолжим до пересечения отрезки DC и PQ . Это можно сделать, так как указанные отрезки лежат в одной плоскости и, как видно из рис. 4.1, не параллельны. Полученная в результате точка S будет лежать в плоскости нижнего основания, так как вся прямая DC лежит в этой плоскости.
Через точки R и S мы теперь проведем след, который оставит плоскость сечения на плоскости нижнего основания. В результате получим точку T . После того как точки T и P соединены, сечение построено.
Несколько усложним задачу.
Пример 2.Построить сечение куба, проходящее через точки P , Q и R , расположенные так, как показано на рис. 4.2.
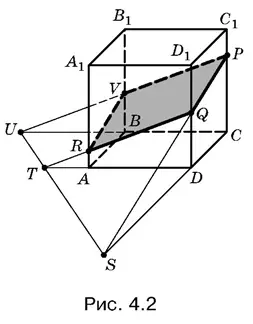
В этом случае одной вспомогательной точки окажется недостаточно. Хотя из рис. 4.2 видно, что сечение не пересечет плоскость нижнего основания, нужно построить след плоскости сечения на нижнем основании. Точку S мы построим так же, как в примере 1, а вторую точку T найдем, продолжив отрезки RQ и AD . След ST пересечет прямую BC в точке U . Так как точки U и P лежат в плоскости сечения, то, соединив их, найдем точку V , принадлежащую сечению куба, которая позволит завершить построение.
Пример 3.Построить сечение куба, проходящее через точку R , расположенную на передней грани куба, и точки P и Q — на ребрах задней его грани (рис. 4.3).
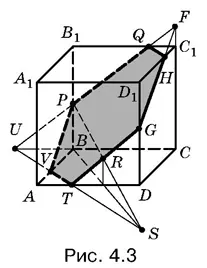
И на этот раз нам поможет построение следа плоскости сечения на плоскости нижнего основания. Чтобы было ясно, что точка R лежит на плоскости передней грани куба, спроецируем ее на основание. Проекция прямой PR и прямая PR пересекутся в точке S , принадлежащей следу. Вторую точку U следа мы получим, продолжив до пересечения BC и PQ . След US пересечет куб по отрезку VТ . Продолжим TR до пересечения с DD 1в точке G . Чтобы закончить построение, получим еще одну вспомогательную точку F так, как это было сделано в первом примере.
Построение теней осуществляется с помощью тех же самых приемов. При этом нужно в качестве вспомогательной точки использовать проекцию источника света на плоскость, на которую падает тень.
Построим, например, тень, отбрасываемую вертикальной спичкой AB на плоскость P (концом В спичка упирается в плоскость), если источник света расположен в точке Q , а точка Q 1есть проекция точки Q на плоскость P (рис. 4.4, а ). Проведем две прямые AQ и BQ 1, пересекающиеся в точке А 1. Отрезок А 1 В и будет тенью спички AB .
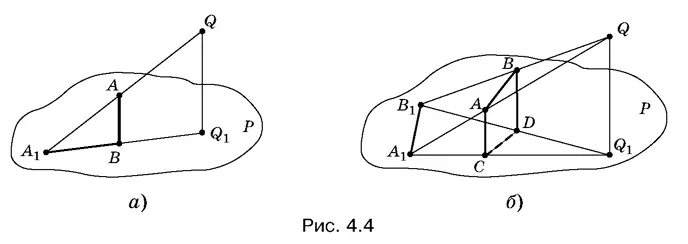
Если спичка AB расположена между плоскостью P и источником света Q произвольным образом, то построение тени показано на рис. 4.4, б . Предполагается, что проекции точек А , В и Q (это точки С , D и Q 1соответственно) на плоскость P заданы или могут быть найдены. Вместо того чтобы строить тень спички AB , мы строим тени А 1 С и В 1 D двух вертикальных спичек AC и ВD , а затем, соединив точки А 1и В 1, получаем нужную тень. Проекция спички AB на плоскость P фактически задана. Это отрезок CD. Тенью, отбрасываемой этой спичкой на плоскость P , если источник света расположен в точке Q , будет отрезок А 1 В 1.
Пример 4.Источник света расположен над плоскостью нижнего основания куба в точке Q на высоте, вдвое превышающей ребро куба (рис. 4.5). Построить тень, отбрасываемую кубом на плоскость его нижнего основания.
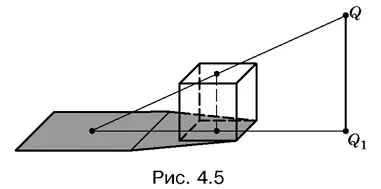
Разумеется, можно было бы построить отдельно тени, отбрасываемые каждым вертикальным ребром куба, а затем соединить соответствующие вершины. Однако здесь проще воспользоваться тем, что ребра верхнего основания куба параллельны плоскости нижнего основания. Следовательно, тенью, отбрасываемой верхним основанием куба, будет квадрат. Поскольку QQ 1вдвое больше ребра куба, то сторона этого квадрата будет равна 2 а (докажите).
Читать дальше
Конец ознакомительного отрывка
Купить книгу
















