Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

3.40.Дана правильная треугольная пирамида SABC ( S — вершина) со стороной основания а и боковым ребром b . Одна сфера с центром в точке O 1касается плоскостей SAB и SAC в точках B и C , а другая сфера с центром в точке О 2касается плоскостей SAC и SBC в точках A и B . Найдите объем пирамиды SO 1 BO 2.

3.41.В конус помещены пять равных шаров. Четыре из них лежат на основании конуса, причем каждый из этих четырех шаров касается двух других, лежащих на основании, и боковой поверхности конуса. Пятый шар касается боковой поверхности конуса и остальных четырех шаров. Найдите объем конуса, если радиусы шаров равны r .

3.42.В основании четырехугольной пирамиды SABCD лежит квадрат ABCD со стороной а . Ребро SD = h перпендикулярно к плоскости основания. Внутри пирамиды лежит цилиндр так, что окружность одного его основания вписана в треугольник SCD, а окружность другого касается грани SAB . Найдите высоту цилиндра.

3.43.В конус вписан куб так, что одно его ребро лежит на диаметре основания конуса, вершины куба, не принадлежащие этому ребру, лежат на боковой поверхности конуса, а центр куба лежит на высоте конуса. Найдите отношение объема конуса к объему куба.

3.44.В правильную усеченную треугольную пирамиду вписан шар радиусом r . Боковое ребро пирамиды равно стороне меньшего основания. Найдите объем пирамиды.

3.45.Два шара радиусом r и один шар радиусом R ( R > r ) лежат на плоскости, касаясь друг друга внешним образом. Найдите радиус шара, касающегося всех шаров и плоскости.

3.46.Два равных шара касаются друг друга и граней двугранного угла. Третий шар меньшего радиуса также касается граней этого двугранного угла и обоих данных шаров. Дано отношение m радиуса меньшего шара к радиусу одного из равных шаров. Найдите величину α двугранного угла. Каким должно быть m , чтобы задача имела решение?

3.47.На плоскости P стоит равносторонний конус, высота которого 10 см. Каждый из трех равных шаров, лежащих на плоскости P вне конуса, касается двух других шаров и боковой поверхности конуса. Найдите радиус шаров.

3.48.На плоскости уложены n равных конусов, имеющих общую вершину в точке, лежащей на этой плоскости. Каждый конус касается двух других конусов. Найдите угол при вершине конуса в осевом сечении.

3.49.Ребро правильного тетраэдра ABCD равно а . На ребре AB , как на диаметре, построена сфера. Найдите радиус сферы, вписанной в трехгранный угол A тетраэдра, если известно, что она касается построенной сферы и ее центр лежит на высоте тетраэдра.

3.50.Правильная пирамида, в основании которой лежит квадрат со стороной а , вращается вокруг прямой, проходящей через ее вершину и параллельной стороне основания. Вычислите объем тела вращения, если плоский угол при вершине пирамиды равен α.

3.51.Полная поверхность конуса в два раза больше поверхности вписанного в него шара. Определите отношение объема конуса к объему шара.

3.52.В основании произвольной (не обязательно прямой) призмы лежит правильный треугольник. Высота призмы равна H . Площади двух боковых граней равны S 1, а площадь третьей равна S 2. Найдите сторону основания. Исследуйте решение.

3.53.Найдите способ, позволяющий вписать в куб сразу четыре пирамиды: две треугольные и две четырехугольные — так, чтобы их суммарный объем был наибольшим.

3.54.Основанием треугольной пирамиды SABC служит правильный треугольник ABC со стороной 6. Высота пирамиды, опущенная из вершины S , равна 4, а основание этой высоты принадлежит основанию ABC , включая его границу. Около пирамиды описали шар радиусом R . Найдите наименьшее возможное значение R , удовлетворяющее условиям задачи [1] Эту задачу нужно решать с особым вниманием. .

Умение правильно построить сечение по трем точкам упрощает решение некоторых геометрических задач.

Прежде чем приступать к решению задач этой главы, разберите несколько примеров на построение сечений и теней.

Пример 1.Построить сечение куба, проходящее через точки P , Q и R , расположенные так, как показано на рис. 4.1.

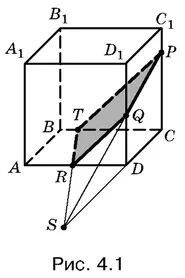
Точки P и Q (и точки Q и R ) можно соединить сразу, так как они лежат в одной из граней куба.