Борис Бирюков - Жар холодных числ и пафос бесстрастной логики

9. Обращаем внимание на то, что мы не стремимся к независимости постулатов нашего аппарата. Например, свойство рефлексивности отношения равенства оказывается в данном построении производным от свойств симметричности и транзитивности этого отношения и каждой из схем аксиом 7, 8, 11—15. Со свойствами отношения равенства можно подробнее ознакомиться по кн.: А. Тарский. Введение в логику и методологию дедуктивных наук. М., 1948, с. 90 и далее. О философских вопросах, связанных в равенством и отождествлением, см: Д. П. Горский. Вопросы абстракции и образование понятий. М., 1961.

10. То есть (а → β) ≝ (~а V β), где ≝ есть знак «равенства выражений по определению» («графического» их совпадения). Мы будем считать, что к равенствам по определению тоже применимы правила [b] (ср. ниже с. 64—65 и 69—70).

11. Различного рода исчисления равенств оказываются весьма полезным инструментом во многих разделах логики и оснований математики (ср. кн.: Р. Л. Гудстеин. Рекурсивный математический анализ. М., 1970, в которой исчисление равенств используется для построения и исследования фрагментов конструктивной математики; о конструктивном направлении в математике см. ниже, гл. 5 и далее). Систематическое представление различных логических систем в виде соответствующих исчислений равенств было осуществлено Г. И. Сыркиным в его курсах лекций «Алгебраические методы в логике», читанных на философском факультете МГУ в 1974—1975 гг. 1

12. Столбцы для аргументов от остальной части таблицы мы отделяем двойной вертикальной чертой. Обращаем внимание на то, что фигурирующие в таблицах 0 и 1 не следует смешивать с константами 0 и 1.

13. С учетом интерпретации констант 0 и 1, которая будет дана ниже.

14. Мы не останавливаемся на некоторых деталях определения;

понятия «верные равенства формул», отсылая читателя к книге П. С. Новикова, указанной в примечании 6.

В этой книге говорится, правда, об отношении «равносильности» формул, но это по существу то же, что мы имеем в виду под совпадением функций (точнее, впрочем, то же, что в следующей интерпретации окажется равенством или равносильностью форм высказываний).

15. Вместо слов «формула а при данных значениях своих переменных переходит в истинное (или ложное) высказывание» мы будем употреблять и такое выражение: «формула а принимает такое-то (истинностное) значение», а также говорить: «формула а истинна (ложна)».

16. В связи с данной интерпретацией заметим, что со знаками → и ≡ можно было с самого начала поступить иначе: не вводить их определениями (как сокращения), а включить в сам язык формальной системы — в ее алфавит (расширив соответствующим образом пункт I в)). Это приведет к расширению понятия формулы и добавлению к системе постулатов схем аксиом для → и ≡. А именно, в пункт II (в) добавляется- «если а и β — формулы, то (а → β) и (а ≡ β) — тоже формулы», а к системе постулатов IV[a] присоединяются: 18. (а → β) = (~а V β) и 19. (а ≡ β) = (~а V β) & (а V ~β)). Пункт V при этом должен быть удален.

17. Ср. формулировку этих законов у Джевонса (с. 43). Очевидно, что способ «формульного» представления этих законов зависит от характера рассматриваемого логического аппарата.

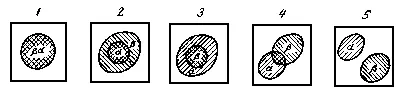
рис. 7. Круговые схемы, изображающие пять возможных отношений между двумя произвольными классами а и β.

18. Аналогично, в школьной математике не пишут, скажем, ((а+b)+с)+d или (а+b)+(с+d) а записывают просто а+b+с+d.

19. Эрнет Шредер (E. Schroder, 1841—1902) является автором трехтомных «Лекций по алгебре логики» (Vorlesungen uber die Logik. Bd. 1-3, Leipzig, 1890—1905), знаменующих собой — вместе с трудами русского логика и астронома П. С. Порецкого (1846—1907) — вершину развития алгебры логики в прошлом столетии. Задача, которая приводится ниже, заимствована из первого тома «Лекций». Эту задачу приводила в своих лекциях по математической логике в Московском университете С. А. Яновская; мы приводим задачу в ее формулировке.

20. Впрочем, операции булевой алгебры можно задавать указанием и других наборов их свойств. О булевых алгебрах см., например:

И. М. Яглом. Алгебра Буля.— В сб.: «О некоторых вопросах современной математики и кибернетики». М., 1965.

21. Напоминаем, что здесь высказывание понимается «классически», то есть как выражение либо истинное, либо ложное, но не то и другое вместе.