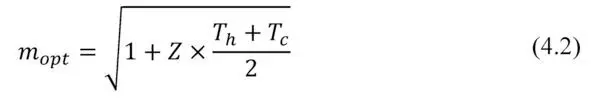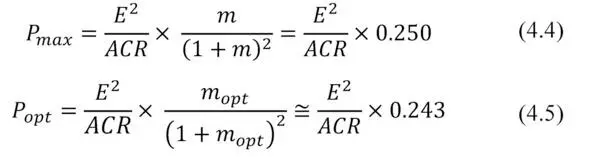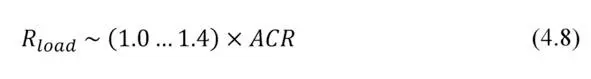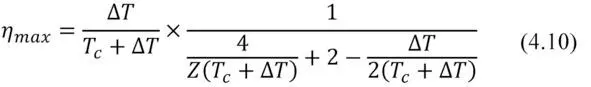Gennady Gromov - Thermoelectric Microgenerators. Optimization for energy harvesting

– On the other side also follows from the equation (3.6) that at the given loading resistance R load , the less internal resistance ACR of generator, then more power P (an example, Fig. 3.2 – an arrow up).

– At the same time, for such generator with smaller resistance ACR , there is even more optimal loading (Fig. 3.2 – arrow sideways) with smaller resistance R load (Fig. 3.2 – red arrow down) which provides even more power.

Maximum power P max conversion occurs when:

And corresponding maximum electric current I max

Comparing (3.2) and (3.3) and (3.7) (3.8) respectively, we get:

– Maximum power P max that can be obtained by thermoelectric generator is only one quarter of the maximum available transformed power by the generator (short circuit capacity).

– Electric current I max through the module in maximum power output is half of short-circuit electric current I sc (3.2).

Introduction.In any heat engine the mode of maximum power differs from the mode of maximum efficiency. In this Chapter the operating mode of thermoelectric generator – maximum efficiency is considered in details.

The value of efficiency η changes with variations of the load resistance R load similarly to dependence of P vs R load (e.g., Fig. 3.1). Namely dependence of efficiency η from the ratio m also has a maximum. But this is not the same point as the maximum P max . The maximum of η takes place at other value of power P opt somewhat different from the P max .

General formula for the efficiency η is the following

Omitting the detailed math (see Chapter 2), it can be shown that in a simplified form the maximal efficiency η opt occurs when

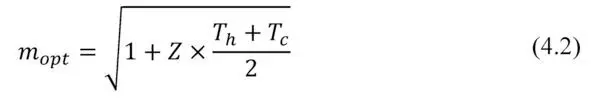
where T h and T c – correspondingly, temperatures of the hot and cold sides of generator; Z – thermoelectric Figure-of-Merit of the generator.

In practice, in applications with small temperature differences and typical Figure-of-Merit of generators, the value m opt given by (4.2) is approximately equal to

With regard to the P max and P opt – they are pretty close each other.

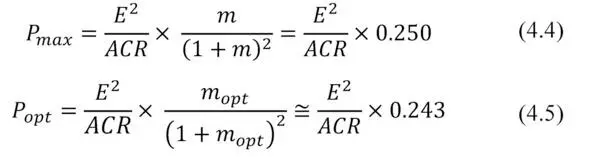
It should be noted that the efficiency η at maximum power mode and at maximum efficiency mode are also close to each other. It can be shown if the corresponding values m max and m opt to apply in formula (4.1), respectively, then

Choosing of practically optimal load resistance between maximum power and maximum efficiency modes can be in the range (Fig. 4.1).

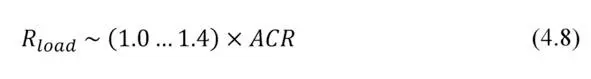
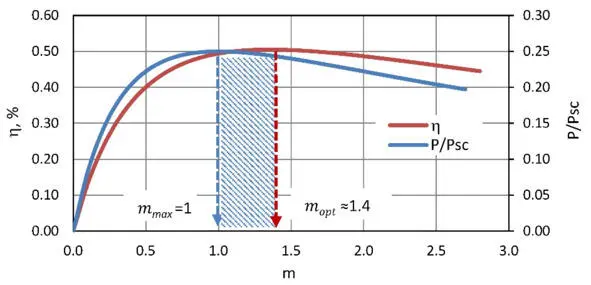
Figure. 4.1 Dependence of the efficiency η and power P related to P scvs ratio m of resistances for two main generator operation modes – maximuum power (P max, m max, η max) and maximum efficiency (P opt, m opt, η opt).

In practice, use the electric load from this range (4.8) turns out to be more comfortable than to select optimal electric load with exactly the specified value.

From the formula (4.1) with use of (4.3) it can be build a useful table for estimates of the absolute value of the maximum efficiency η opt of thermoelectric generator depending on temperature difference Δ T (Table 4.1).

Table 4.1 Dependence* of maximum efficiency η opt vs temperature difference ΔT on a generator.

The common conclusions from formula (4.1) and Table 4.1 are the following:

– in practice, the efficiency η opt is almost a linear function of the temperature difference Δ T.

– one degree of the temperature difference Δ T gives about 0.05% of maximum efficiency η opt .

Useful information on the efficiency of thermoelectric generator should be of the following formulas for two marginal efficiency modes: the maximum efficiency mode η opt and the maximum power mode η max .

For these modes the efficiency η can be written as the following:

– for maximum efficiency mode η opt

– for maximum power mode η max

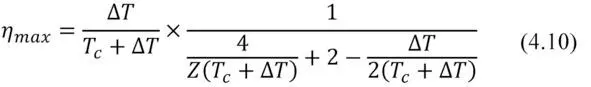
In both formulas (4.9) and (4.10) the first fractional multiplier is, generally speaking, the ideal Carnot cycle efficiency ( ∆ T/T h) . The second multiplier – thermoelectric factor reduces ideal efficiency of the Carnot cycle.

So, near room temperature ( T c≃ 300K) and typical Z≃0.003K -1 we have an numerical expression for the maximal efficiency η opt

As for the mode of maximum power efficiency η max , correspondingly:

In other words, state-of-art thermoelectric microgenerators provide efficiency only 15.5—16% of the ideal Carnot cycle efficiency.