Gennady Gromov - Thermoelectric Microgenerators. Optimization for energy harvesting

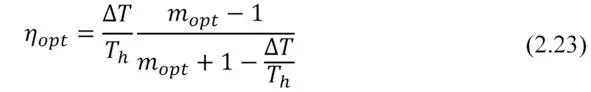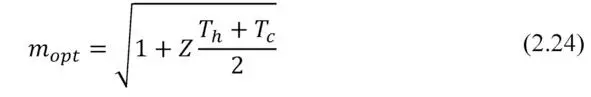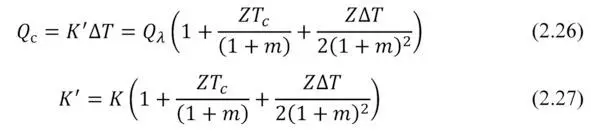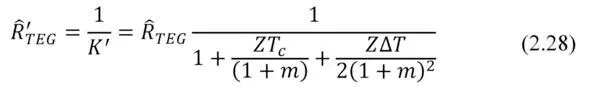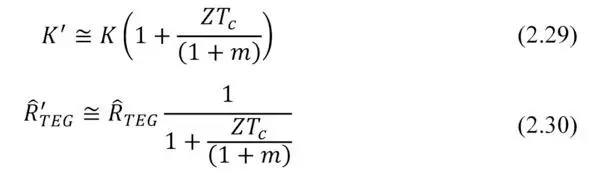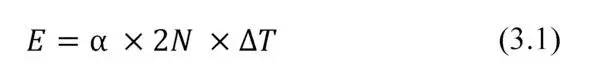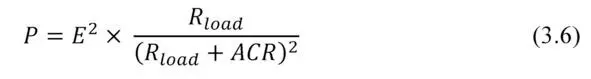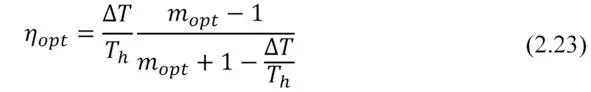
Where the optimum ratio of load and internal resistances m opt ( m opt=R load/ACR ) can be expressed as the following.

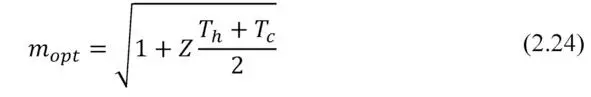
Note, please, the formula (2.24). If maximum power P max converted by generator can be achieved when m =1, then maximum efficiency η – at other value of this ratio – m opt (2.24). In the thermoelectric generator, as in any heat engine, maximum power mode operation differs from mode of maximum efficiency.

Heat Q passed through a media, which is the generator, one can write in general using the effective thermal conductivity K” of this media and temperature difference Δ T as the following.

In working generator the heat is Q c (2.12), which differs from the heat transported due to “simple” thermal conductivity Q λ:

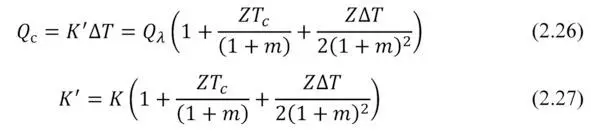
Effective thermal conductivity K” differs from conventional thermal conductivity K of agenerator due to the additional Peltier and Joule heat flows, that appear in the working generator, and which are superimposed on the conventional thermal conductivity (Fig. 2.2).

Thermal resistance of the working generator Ȓ’ TEG is the following

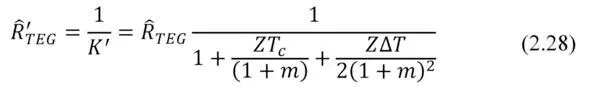
To a first approximation, at small temperature differences Δ T the 3-rd member (Joule) in the sum in brackets (2.27) can be ignored. Indeed, it can be shown that contribution of this term at small temperature differences is small, no more than 0.5—1%.

Then

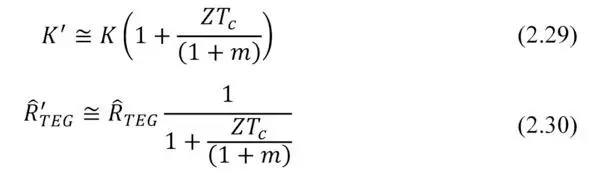
Exclusion of a member, depending on Δ T dramatically simplifies analysis of a thermoelectric generator in the tasks of complex ambient. Where the generator is placed between other media and interfaces with different thermal resistance, and it is desirable to optimize the thermal resistance Ȓ’ TEG of the working generator (see Chapter 5).

When open electrical circuit takes place in the generator, then there is no Peltier and no Joule heat flows. Only thermal conductivity heat flow takes place. In other words, then R load=∞ and m=∞ then the formula (2.26) is simplified to:

Temperature difference Δ T at a generator module when an open circuit takes place is associated with heat flow of thermal contuctivity Q λ as the following.

Preface. Thermoelectric generator transforms thermal energy and gives it to external electric circuit. Here coordination of elements of the electric circuit with parameters of the generator is essential for extraction of maximum power. In this Chapter questions of optimization of the electric circuit are considered.

Simplified electrical circuit of a generator module is shown in Fig.3.1.

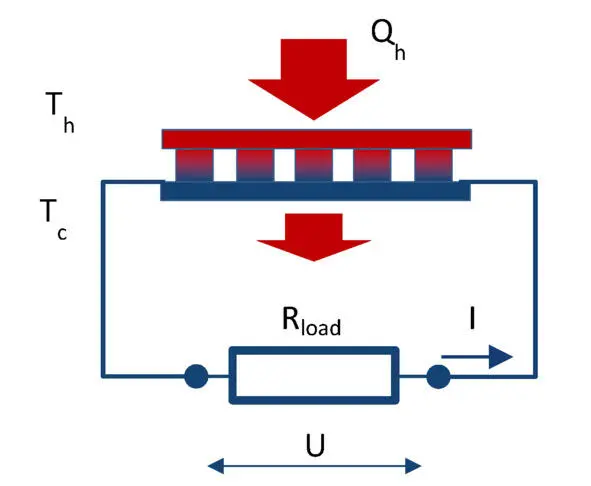
Figure. 3.1 Schematics of thermoelectric generator.

Maximum electric power transformed by a generator from heat source is defined by thermoEMF E and internal resistance ACR of the generator.

The thermoEMF E is found as the following

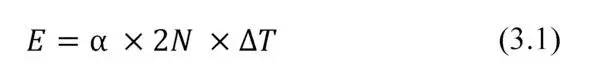
where α – thermoelectric coefficient (Seebeck coefficient) of pair of thermoelements n- and p-types; 2N – number of elements in generator module; Δ T -working temperature difference on generator module ( Δ T=T h-T c).

If to short the electric circuit of the generator ( R load= 0), the short-circuit current I sc is

At short-circuit the power P sc allocated in the electric circuit is maximal.

However, all this power will be converted into Joule heat in thermoelements of the generator. In fact, heat converted into electric current returns again into the heat. There is no useful work.

A generator performs useful work when converted power is given out to the external load that has electrical resistance different from zero ( R load> 0) .

Then the working current I in the electric circuit (Fig. 3.1) is

Voltage U in the electric circuit, correspondingly

Formula of the net power P has the following form:

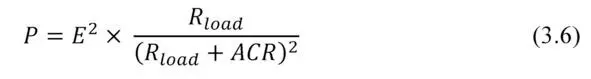
From equation (3.6) it follows that the generated power P nonlinearly dependends on the load resistance R load .

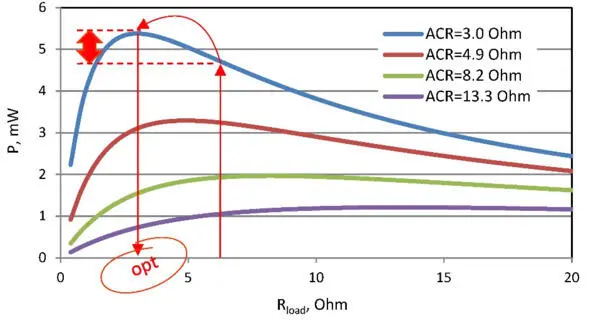
Figure. 3.2 Sample dependence of generator power (four variants by ACR) from the load resistance. Temperature difference 5°C.

This dependence has maximum power P max when external load resistance R load is equal to internal resistance ACR of the generator ( R load=ACR):

– At given internal resistance ACR of generator, there is an optimal load resistance R load in terms of maximum power conversion.